
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F. 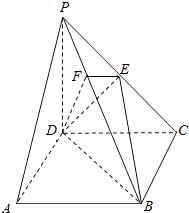
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
【答案】
(1)证明:连接AC,AC交BD于O.连接EO.
∵底面ABCD是正方形,∴点O是AC的中点.
∴在△PAC中,EO是中位线,∴PA∥EO,
∵EO平面EDB,且PA平面EDB,
∴PA∥平面EDB
(2)证明:∵PD⊥底面ABCD,且DC底面ABCD,∴PD⊥BC.
∵底面ABCD是正方形,∴DC⊥BC,
∴BC⊥平面PDC.∵DE平面PDC,∴BC⊥DE.
又∵PD=DC,E是PC的中点,∴DE⊥PC.∴DE⊥平面PBC.
∵PB平面PBC,∴DE⊥PB.又∵EF⊥PB,且DE∩EF=E,
∴PB⊥平面EFD.
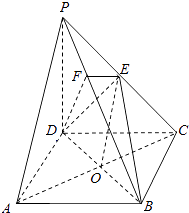
【解析】(1)由题意连接AC,AC交BD于O,连接EO,则EO是中位线,证出PA∥EO,由线面平行的判定定理知PA∥平面EDB;(2)由PD⊥底面ABCD得PD⊥DC,再由DC⊥BC证出BC⊥平面PDC,即得BC⊥DE,再由ABCD是正方形证出DE⊥平面PBC,则有DE⊥PB,再由条件证出PB⊥平面EFD.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点. 
(1)证明:MN∥平面PAD;
(2)若PB与平面ABCD所成的角为45°,求三棱锥C﹣BDN的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}与{bn},若a1=3且对任意正整数n满足an+1﹣an=2,数列{bn}的前n项和Sn=n2+an .
(1)求数列{an},{bn}的通项公式;
(2)求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1= ![]() ,∠ABC=60°.
,∠ABC=60°. 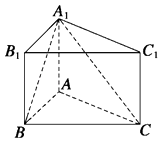
(1)证明:AB⊥A1C;
(2)(理)求二面角A﹣A1C﹣B的余弦值大小.
(文)求此棱柱的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
, ![]() .试判断
.试判断![]() ,
, ![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,若sin(A+B﹣C)=sin(A﹣B+C),则△ABC必是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com