
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
【答案】(1)![]() (2)①见解析②推荐该商场选择乙厂家长期销售
(2)①见解析②推荐该商场选择乙厂家长期销售
【解析】试题分析:
(1)利用题中所给数据可得一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率为
的概率为![]() ;
;
(2)首先确定![]() 可能的取值回味
可能的取值回味![]() ,分别求得概率值,最后计算数学期望为
,分别求得概率值,最后计算数学期望为![]() ;
;
(3)利用题意首先求得甲的平均值,然后求解甲乙的日平均返利额即可得出结论.
试题解析:
解:(1)记“抽取的两天中一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() ”为事件
”为事件![]() ,则
,则![]()
(2) ①设乙产品的日期销售量为![]() ,则当
,则当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
, ![]() 的所有可能取值为:
的所有可能取值为: ![]()
![]() 的分别列为:
的分别列为:
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
②依题意,甲厂家的日平均销售量为:
![]() ,
,
所以甲厂家的日平均返利额为: ![]() 元,由①得乙厂家的日平均返利额为
元,由①得乙厂家的日平均返利额为![]() 元,(大于
元,(大于![]() 元),所以推荐该商场选择乙厂家长期销售.
元),所以推荐该商场选择乙厂家长期销售.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2< ![]() <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F. 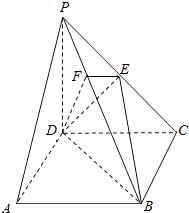
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 能否为等差数列?若能,求其通项公式;若不能,试说明理由;
能否为等差数列?若能,求其通项公式;若不能,试说明理由;
(3)若数列![]() 是各项均为正整数的递增数列,设
是各项均为正整数的递增数列,设![]() ,则当
,则当![]() ,
, ![]() ,
, ![]() 和
和![]() ,
, ![]() ,
, ![]() 均成等差数列时,求正整数
均成等差数列时,求正整数![]() ,
, ![]() ,
, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ![]() ,且过点D(2,0).
,且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点 ![]() ,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 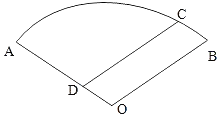
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=6,若x0是方程f(x)﹣f′(x)=4的一个解,且x0∈(a,a+1)(a∈N*),则实数a=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com