
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 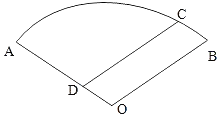
【答案】解:法一:设该扇形的半径为r米,连接CO. 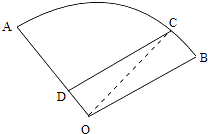
由题意,得CD=500(米),DA=300(米),∠CDO=60°
在△CDO中,CD2+OD2﹣2CDODcos60°=OC2
即, ![]()
解得 ![]() (米)
(米)
答:该扇形的半径OA的长约为445米.
法二:连接AC,作OH⊥AC,交AC于H,
由题意,得CD=500(米),AD=300(米),∠CDA=120°
在△CDO中,AC2=CD2+AD2﹣2CDADcos120°= ![]() .
.
∴AC=700(米).![]() .
.
在直角△HAO中,AH=350(米), ![]() ,
,
∴ ![]() (米).
(米).
答:该扇形的半径OA的长约为445米.
【解析】连接OC,由CD∥OB知∠CDO=60°,可由余弦定理得到OC的长度.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
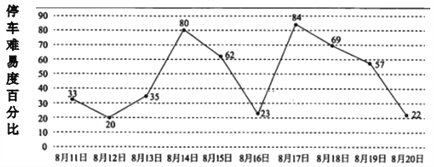
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设![]() 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2 , a4的等差中项. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog2an , 其前n项和为Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,若sin(A+B﹣C)=sin(A﹣B+C),则△ABC必是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c(b,c∈R),并设 ![]() ,
,
(1)若F(x)图像在x=0处的切线方程为x﹣y=0,求b、c的值;
(2)若函数F(x)是(﹣∞,+∞)上单调递减,则 ①当x≥0时,试判断f(x)与(x+c)2的大小关系,并证明之;
②对满足题设条件的任意b、c,不等式f(c)﹣Mc2≤f(b)﹣Mb2恒成立,求M的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com