
【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
【答案】
(1)证明:tanα+2cot2α=tanα+ ![]()
=tanα+2× ![]()
=tanα+ ![]() ﹣tanα
﹣tanα
=cotα,
∴cotα=tanα+2cot2α.
(2)证明:∵cotα=tanα+2cot2α,
∴tanα+2tan2α+4cot4α
=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α
=cotα,
∴cotα=tanα+2tan2α+4cot4α
(3)证明:一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N*.
证明:∵cotα=tanα+2cot2α,∴cot2α=tan2α+2cot4α,
∴cotα=tanα+2tan2α+4cot4α=tanα+2tan2α+22cot22α,
以此类推得cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N*
(4)解:tan5°+2tan10°+4tan20°+8tan50°
=tan5°+2tan10°+4tan20°+8cot40°
=cot5°.
【解析】(1)tanα+2cot2α=tanα+2× ![]() ,由此能证明cotα=tanα+2cot2α.(2)由cotα=tanα+2cot2α,得到tanα+2tan2α+4cot4α=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α,由此能证明cotα=tanα+2tan2α+4cot4α.(3)一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N* . 再由合情推量进行证明.(4)利用(3)的一般结论直接化简.
,由此能证明cotα=tanα+2cot2α.(2)由cotα=tanα+2cot2α,得到tanα+2tan2α+4cot4α=cotα﹣2cot2α+2cos2α﹣4cot4α+4cot4α,由此能证明cotα=tanα+2tan2α+4cot4α.(3)一般地,cotα=tanα+2tan2α+22tan22α+…+2n﹣1tan2n﹣1α+2ncot2nα,n∈N* . 再由合情推量进行证明.(4)利用(3)的一般结论直接化简.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 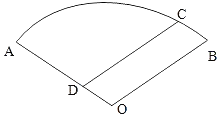
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.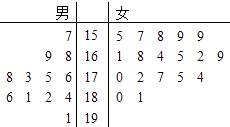
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为参数.
为参数.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 极值点的个数,并说明理由;
极值点的个数,并说明理由;
(3)若对任意![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个分段函数可利用函数 ![]() 来表示,例如要表示一个分段函数
来表示,例如要表示一个分段函数 ![]() ,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
(1)求函数f(x)在区间[0,4]上的最大值与最小值;
(2)若关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com