
【题目】已知一个分段函数可利用函数 ![]() 来表示,例如要表示一个分段函数
来表示,例如要表示一个分段函数 ![]() ,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
(1)求函数f(x)在区间[0,4]上的最大值与最小值;
(2)若关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立,求实数k的取值范围.
【答案】
(1)解:由题意可知 ![]() ,
,
当1≤x≤4时,f(x)=﹣(x﹣2)2+1,则f(x)在[1,2]上递增,在[2,4]上递减;
当0≤x<1时,f(x)=x2﹣1,则f(x)在[0,1)上递增,
而f(0)=﹣1,f(2)=1,f(4)=﹣3,所以f(x)max=f(2)=1,f(x)min=f(4)=﹣3
(2)解:由图可知,
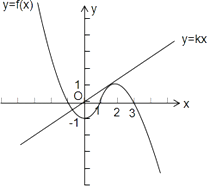
当直线y=kx与抛物线y=﹣x2+4x﹣3只有一个交点时,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0,得(k﹣4)2﹣12=0,得k=4±2 ![]() ,
,
结合图像,可知当k≥4﹣2 ![]() 时,关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立
时,关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立
【解析】(1)由题意可知 ![]() ,利用二次函数的单调性可求得函数f(x)在区间[0,4]上的最大值与最小值;(2)在同一坐标系中作出y=f(x)与y=kx的图像,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0可求得k的值,结合图像可求得,对任意x∈[0,+∞)都成立时,实数k的取值范围.
,利用二次函数的单调性可求得函数f(x)在区间[0,4]上的最大值与最小值;(2)在同一坐标系中作出y=f(x)与y=kx的图像,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0可求得k的值,结合图像可求得,对任意x∈[0,+∞)都成立时,实数k的取值范围.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈N,f(x)=(1+x)m+(1+x)n .
(1)当m=n=5时,若 ![]() ,求a0+a2+a4的值;
,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c(b,c∈R),并设 ![]() ,
,
(1)若F(x)图像在x=0处的切线方程为x﹣y=0,求b、c的值;
(2)若函数F(x)是(﹣∞,+∞)上单调递减,则 ①当x≥0时,试判断f(x)与(x+c)2的大小关系,并证明之;
②对满足题设条件的任意b、c,不等式f(c)﹣Mc2≤f(b)﹣Mb2恒成立,求M的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)在(0,+∞)上是增函数,且f( ![]() )=0,则不等式xf(x)>0的解集是( )
)=0,则不等式xf(x)>0的解集是( )
A.(0, ![]() )
)
B.( ![]() ,+∞)??
,+∞)??
C.(﹣ ![]() ,0)∪(
,0)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣ ![]() )∪(0,
)∪(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义在[﹣1,2]上的函数f(x)的图象为折线段ACB, 
(1)求函数f(x)的解析式;
(2)请用数形结合的方法求不等式f(x)≥log2(x+1)的解集,不需要证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
, ![]() (其中
(其中![]() 为常数).
为常数).
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,求证:
时,求证: ![]() (其中e为自然对数的底数).
(其中e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知设函数f(x)=loga(1+2x)﹣loga(1﹣2x)(a>0,a≠1).
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)求使f(x)>0的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com