
【题目】已知函数f(x)=lg(mx2+mx+1),若此函数的定义域为R,则实数m的取值范围是;若此函数的值域为R,则实数m的取值范围是 .
【答案】[0,4);[4,+∞)
【解析】解:(1.)∵函数f(x)=lg(mx2+mx+1)的定义域为R,∴mx2+mx+1>0在R上恒成立,
①当m=0时,有1>0在R上恒成立,故符合条件;
②当m≠0时,由 ![]() ,
,
解得0<m<4,
综上,实数m的取值范围是[0,4).
(2.)令g(x)=mx2+mx+1的值域为A,
∵函数f(x)=lg(mx2+mx+1)的值域为R,
∴(0,+∞)A,
当m=0时,g(x)=1值域不是为R,不满足条件;
当m≠0时, ![]() ,解得:m≥4,
,解得:m≥4,
所以答案是:[0,4),[4,+∞).
【考点精析】关于本题考查的函数的定义域及其求法,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为参数.
为参数.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 极值点的个数,并说明理由;
极值点的个数,并说明理由;
(3)若对任意![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
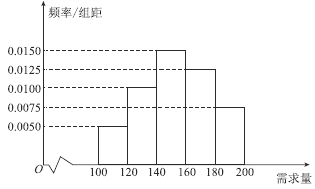
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个分段函数可利用函数 ![]() 来表示,例如要表示一个分段函数
来表示,例如要表示一个分段函数 ![]() ,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
(1)求函数f(x)在区间[0,4]上的最大值与最小值;
(2)若关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b﹣1)(a≠0).
(1)当a=1,b=2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若f(x)的两个不动点为x1 , x2 , 且f(x1)+x2= ![]() ,求实数b的取值范围.
,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,且
,且![]() ,矩形
,矩形![]() 底面
底面![]() ,
,![]() 为线段
为线段![]() 上一动点,满足
上一动点,满足![]() .
.

(Ⅰ)若![]() 平面
平面![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,锐二面角
时,锐二面角![]() 的余弦值为
的余弦值为![]() ,求多面体
,求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com