
【题目】已知函数f(x)=sinx+ ![]() cosx.求:
cosx.求:
(1)f(x)图象的对称中心的坐标;
(2)f(x)的单调区间.
【答案】
(1)解:函数f(x)=sinx+ ![]() cosx=2sin(x+
cosx=2sin(x+ ![]() ),
),
令x+ ![]() =kπ,求得x=kπ﹣
=kπ,求得x=kπ﹣ ![]() ,可得函数的图象的对称中心为(kπ﹣
,可得函数的图象的对称中心为(kπ﹣ ![]() ,0),k∈Z
,0),k∈Z
(2)解:令2kπ﹣ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得2kπ﹣
,求得2kπ﹣ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,
,
可得函数的增区间为[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z;
],k∈Z;
令2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得2kπ+
,求得2kπ+ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,
,
可得函数的增区间为[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
【解析】(1)利用两角和的正弦公式化简函数的解析式,再利用正弦函数的图象的对称中心,求得f(x)图象的对称中心的坐标.(2)利用正弦函数的单调性求得f(x)的单调区间.
【考点精析】掌握两角和与差的正弦公式是解答本题的根本,需要知道两角和与差的正弦公式:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}与{bn},若a1=3且对任意正整数n满足an+1﹣an=2,数列{bn}的前n项和Sn=n2+an .
(1)求数列{an},{bn}的通项公式;
(2)求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2 , a4的等差中项. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog2an , 其前n项和为Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为( ) 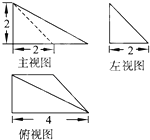
A.10+4 ![]() ?+4
?+4 ![]()
B.10+2 ![]() ?+4
?+4 ![]() ??
??
C.14+2 ![]() ?+4
?+4 ![]()
D.14+4 ![]() ?+4
?+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,若sin(A+B﹣C)=sin(A﹣B+C),则△ABC必是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈N,f(x)=(1+x)m+(1+x)n .
(1)当m=n=5时,若 ![]() ,求a0+a2+a4的值;
,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,定义在[﹣1,2]上的函数f(x)的图象为折线段ACB, 
(1)求函数f(x)的解析式;
(2)请用数形结合的方法求不等式f(x)≥log2(x+1)的解集,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com