
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ![]() ,且过点D(2,0).
,且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点 ![]() ,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
【答案】
(1)解:由题意知椭圆的焦点在x轴上,设椭圆的标准方程是 ![]()
∵椭圆经过点D(2,0),左焦点为 ![]() ,
,
∴a=2, ![]() ,可得b=
,可得b= ![]() =1
=1
因此,椭圆的标准方程为 ![]()
(2)解:设点P的坐标是(x0,y0),线段PA的中点为M(x,y),
由根据中点坐标公式,可得 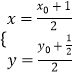 ,整理得
,整理得 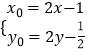 ,
,
∵点P(x0,y0)在椭圆上,
∴可得 ![]() ,化简整理得
,化简整理得 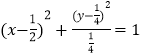 ,
,
由此可得线段PA中点M的轨迹方程是 ![]()
【解析】(1)设椭圆方程为 ![]() ,根据题意可得a=2且c=
,根据题意可得a=2且c= ![]() ,从而b=
,从而b= ![]() =1,得到椭圆的标准方程;(2)设点P(x0 , y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0 , y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.
=1,得到椭圆的标准方程;(2)设点P(x0 , y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0 , y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.


科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员的5次测试成绩如下图所示:
甲 | 茎 | 乙 |
5 7 | 1 | 6 8 |
8 8 2 | 2 | 3 6 7 |
设s1 , s2分别表示甲、乙两名运动员测试成绩的标准差, ![]() 分别表示甲、乙两名运动员测试成绩的平均数,则有( )
分别表示甲、乙两名运动员测试成绩的平均数,则有( )
A.![]() ,s1<s2
,s1<s2
B.![]() ,s1>s2
,s1>s2
C.![]() ,s1>s2
,s1>s2
D.![]() ,s1=s2
,s1=s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1= ![]() ,∠ABC=60°.
,∠ABC=60°. 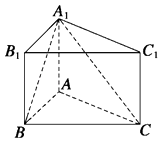
(1)证明:AB⊥A1C;
(2)(理)求二面角A﹣A1C﹣B的余弦值大小.
(文)求此棱柱的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,已知a1=1, ![]() ,
,
(1)求证数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)若对一切n∈N* , 等式a1b1+a2b2+a3b3+…+anbn=2n恒成立,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
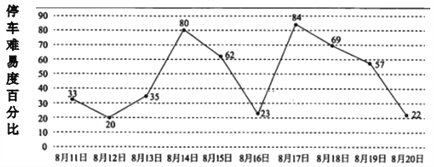
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设![]() 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2 , a4的等差中项. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog2an , 其前n项和为Sn , 若(n﹣1)2≤m(Sn﹣n﹣1)对于n≥2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(x+φ)的图象上每点的横坐标缩短为原来的 ![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位长度后得到的图象关于坐标原点对称,则下列直线中是函数f(x)图象的对称轴的是( )
个单位长度后得到的图象关于坐标原点对称,则下列直线中是函数f(x)图象的对称轴的是( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com