
| A. | [$\frac{1}{2}$,2] | B. | [-$\frac{1}{2}$,2] | C. | [0,2] | D. | [0,$\frac{1}{2}$] |
分析 利用对数函数的单调性求解即可.
解答 解:函数f(x)=log${\;}_{\frac{1}{2}}$x,x∈[$\frac{1}{4}$,$\frac{\sqrt{2}}{2}$],是减函数,
所以函数的最小值为:f($\frac{\sqrt{2}}{2}$)=log${\;}_{\frac{1}{2}}$$\frac{\sqrt{2}}{2}$=$\frac{1}{2}$,
函数的最大值为:f($\frac{1}{4}$)=log${\;}_{\frac{1}{2}}$$\frac{1}{4}$=2.
函数的值域为:[$\frac{1}{2}$,2].
故选:A.
点评 本题考查对数函数的单调性与最值的求法,考查计算能力.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
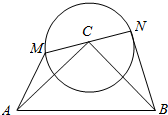 Rt△ABC中,∠C=90°,AC=BC=2,⊙C的半径是1,MN是⊙C直径,求:$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系.
Rt△ABC中,∠C=90°,AC=BC=2,⊙C的半径是1,MN是⊙C直径,求:$\overrightarrow{AM}$•$\overrightarrow{BN}$的最大值及此时$\overrightarrow{MN}$与$\overrightarrow{AB}$的关系.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com