
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
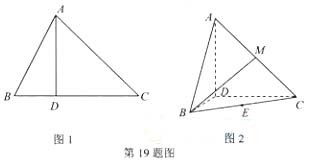
如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示),
(1)当BD的长为多少时,三棱锥A-BCD的体积最大;
(2)当三棱锥A-BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线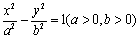 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于A, B两点, O为坐标
的准线分别交于A, B两点, O为坐标 原点. 若双曲线的离心率为2, △AOB的面积为
原点. 若双曲线的离心率为2, △AOB的面积为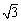 , 则p = ( )
, 则p = ( )
(A) 1 (B) 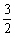 (C) 2 (D) 3
(C) 2 (D) 3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线C: 的左、右焦点分别为
的左、右焦点分别为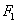 、
、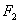 ,离心率为3,直线
,离心率为3,直线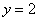 与C的两个交点间的距离为
与C的两个交点间的距离为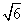 .
.
(Ⅰ)求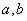 ;
;
(Ⅱ)设过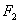 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且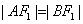 ,证明:
,证明: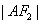 、
、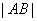 、
、 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
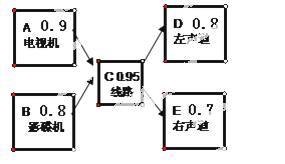
.已知某音响设备由五个部件组成,A电视机,B影碟机,C 线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D
线路,D左声道和E右声道,其中每个部件工作的概率如图所示,能听到声音,当且仅当A与B中有一个工作,C工作,D与E中有一个工作;且若D 和E同时工作则有立体声效果. 能听到立体声效果的概率求听不到声音的概率分别为( ).(结果精确到0.01)
和E同时工作则有立体声效果. 能听到立体声效果的概率求听不到声音的概率分别为( ).(结果精确到0.01)
A. 0.52 0.13 B.0.13 0.52 C. 0.5 0.1 D. 0.45 0.23
查看答案和解析>>
科目:高中数学 来源: 题型:
设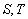 是
是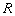 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:
满足:
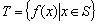 ;
;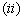 对任意
对任意 ,当
,当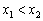 时,恒有
时,恒有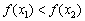 ,那么称这两个集
,那么称这两个集 合“保序同构”,以下集合对不是“保序同构”的是( )
合“保序同构”,以下集合对不是“保序同构”的是( )
A. 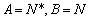 B.
B. 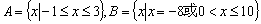
C. 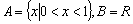 D.
D. 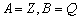
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com