
【题目】已知四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:面![]() 面
面![]() ;
;
(2)求![]() 与
与![]() 夹角的余弦值;
夹角的余弦值;
(3)求面![]() 与面
与面![]() 所成二面角余弦值的大小.
所成二面角余弦值的大小.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)证明面![]() 面
面![]() ,只需证明平面
,只需证明平面![]() 内的直线
内的直线![]() 垂直于平面
垂直于平面![]() 内的相交直线
内的相交直线![]() 即可;(2)建立空间直角坐标系,求得
即可;(2)建立空间直角坐标系,求得![]() ,
,![]() ,利用向量所成的角,即可求解异面直线
,利用向量所成的角,即可求解异面直线![]() 与
与![]() 夹角的余弦值;(3)作在
夹角的余弦值;(3)作在![]() 上取一点
上取一点![]() ,则存在
,则存在![]() ,使
,使![]() ,得
,得![]() ,
,![]() .所以
.所以![]() 为所求二面角的平面角,即可利用向量所成角的公式,求解面
为所求二面角的平面角,即可利用向量所成角的公式,求解面![]() 与面
与面![]() 所成二面角余弦值的大小.
所成二面角余弦值的大小.
试题解析:
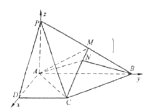
证明:以![]() 为坐标原点
为坐标原点![]() 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)证明:因![]() ,
,![]() ,故
,故![]() ,所以
,所以![]() .
.
由题设知![]() ,且
,且![]() 与
与![]() 是平面
是平面![]() 内的两条相交直线,由此得
内的两条相交直线,由此得![]() 面
面![]() ,
,
又![]() 在面
在面![]() 上,故面
上,故面![]() 面
面![]() .
.
(2)解:因![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,
所以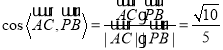 .
.
(3)解:在![]() 上取一点
上取一点![]() ,则存在
,则存在![]() ,使
,使![]() ,
,
![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
要使![]() ,只需
,只需![]() ,即
,即![]() ,解得
,解得![]() .
.
可知当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,能使
,能使![]() .
.
此时,![]() ,
,![]() ,有
,有![]() .
.
由![]() ,
,![]() ,得
,得![]() ,
,![]() .
.
所以![]() 为所求二面角的平面角.
为所求二面角的平面角.
∵![]() ,
,![]() ,
,![]() ,
,
∴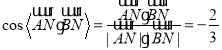


科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A,B两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中
①设![]() 为两个定点,
为两个定点,![]() 为非零常数,
为非零常数,![]() ,则动点
,则动点![]() 的轨迹为双曲线;
的轨迹为双曲线;
②方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③设定圆![]() 上一定点
上一定点![]() 作圆的动点弦
作圆的动点弦![]() ,
,![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④过点![]() 作直线,使它与抛物线
作直线,使它与抛物线![]() 仅有一个公共点,这样的直线有3条;
仅有一个公共点,这样的直线有3条;
其中真命题的序号为_________________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的烟火名目繁多,花色品种繁杂.其中“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如下表:
(单位:秒)存在函数关系,并得到相关数据如下表:

(1)根据上表数据,从下列函数中,选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系:![]() ,确定此函数解析式,并简单说明理由;
,确定此函数解析式,并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求出此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.
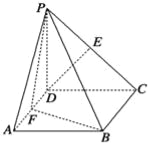
(1)证明:DE∥平面PFB;
(2)求三棱锥A﹣PFB的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com