
【题目】已知![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() 时,
时,![]()
(1)求函数![]() 的解析式.
的解析式.
(2)画出函数![]() 的图象,并写出函数
的图象,并写出函数![]() 单调区间及值域.
单调区间及值域.
【答案】(1) 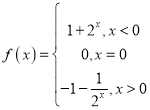 (2) 单调增区间为(-∞,0),(0,+∞);值域为{y|1<y<2或-2<y<-1或y=0}
(2) 单调增区间为(-∞,0),(0,+∞);值域为{y|1<y<2或-2<y<-1或y=0}
【解析】
试题分析:(1)由函数为奇函数可得![]() ,将
,将![]() 转化为
转化为![]() ,代入函数式,结合奇偶性可求得函数解析式;(2)利用函数图像可得到单调区间及值域
,代入函数式,结合奇偶性可求得函数解析式;(2)利用函数图像可得到单调区间及值域
试题解析:(1)因为y=f(x)是定义在R上的奇函数,所以f(-0)=-f(0),所以f(0)=0,
因为x<0时,f(x)=1+2x,所以x>0时,f(x)=-f(-x)=-(1+2-x)=-1-![]() ,
,
所以f(x)=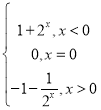
(2)函数f (x)的图象为
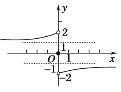
根据f(x)的图象知:
f(x)的单调增区间为(-∞,0),(0,+∞);
值域为{y|1<y<2或-2<y<-1或y=0}.


科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是 ( )
A. 经过正方体任意两条面对角线,有且只有一个平面
B. 经过正方体任意两条体对角线,有且只有一个平面
C. 经过正方体任意两条棱,有且只有一个平面
D. 经过正方体任意一条体对角线与任意一条面对角线,有且只有一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
分数区间 | 甲班频率 | 乙班频率 |
| 0.1 | 0.2 |
| 0.2 | 0.2 |
| 0.3 | 0.3 |
| 0.2 | 0.2 |
| 0.2 | 0.1 |
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的![]() ×
×![]() 列联表:
列联表:
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
参考公式: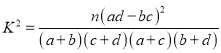 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6月23日15时前后,江苏盐城市阜宁、射阳等地突遭强冰雹、龙卷风双重灾害袭击,风力达12级.灾害发生后,有甲、乙、丙、丁4个轻型救援队从A,B,C,D四个不同的方向前往灾区.已知下面四种说法都是正确的.
(1)甲轻型救援队所在方向不是C方向,也不是D方向;
(2)乙轻型救援队所在方向不是A方向,也不是B方向;
(3)丙轻型救援队所在方向不是A方向,也不是B方向;
(4)丁轻型救援队所在方向不是A方向,也不是D方向;
此外还可确定:如果丙所在方向不是D方向,那么甲所在方向就不是A方向,有下列判断:
①甲所在方向是B方向;②乙所在方向是D方向;③丙所在方向是D方向;④丁所在方向是C方向.
其中判断正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
A. 2 B. 3 C. 6 D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com