解:(Ⅰ)当k=0时,f(x)=e
2x-1-2x,
f
′(x)=2e
2x-2,
令f
′(x)>0,则2e
2x-2>0,解得:x>0.
令f
′(x)<0,则2e
2x-2<0,解得:x<0.
所以,函数f(x)=e
2x-1-2x的单调增区间为(0,+∞).
单调减区间为(-∞,0).
(Ⅱ)由函数f(x)=e
2x-1-2x-kx
2,
则f
′(x)=2e
2x-2kx-2=2(e
2x-kx-1),
令g(x)=e
2x-kx-1,
则g
′(x)=2e
2x-k.
由x≥0,
所以,①当k≤2时,g
′(x)≥0,g(x)为增函数,而g(0)=0,
所以g(x)≥0,即f
′(x)≥0,所以f(x)在[0,+∞)上为增函数,
而f(0)=0,所以f(x)≥0在[0,+∞)上恒成立.
②当k>2时,令g
′(x)<0,即2e
2x-k<0,则0≤x<
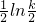
.
即g(x)在[0,
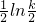
)上为减函数,而g(0)=0,所以,g(x)在[0,
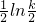
)上小于0.
即f
′(x)<0,所以,f(x)在[0,
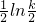
)上为减函数,而f(0)=0,故此时f(x)<0,不合题意.
综上,k≤2.
(Ⅲ)
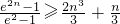
.
事实上,由(Ⅱ)知,f(x)=e
2x-1-2x-2x
2在[0,+∞)上为增函数,
所以,e
2x≥2x
2+2x+1=x
2+(x+1)
2,
则e
0≥1
2e
2≥1
2+2
2e
4≥2
2+3
2e
6≥3
2+4
2…
e
2(n-1)≥(n-1)
2+n
2累加得:1+e
2+e
4+e
6+…+e
2(n-1)≥2(1
2+2
2+3
2+…+(n-1)
2)+n
2.
即
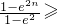
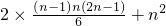
.
所以,
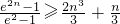
.
分析:(Ⅰ)取x=0后,求出函数的导函数,由导函数大于0和导函数小于0分别求出函数的单调区间;
(Ⅱ)求出原函数的导函数,以k≤2和k>2进行分类讨论,由k≤2时,说明原函数在[0,+∞)上为增函数,说明f(x)≥0在[0,+∞)上恒成立,k>2时,说明这种情况不存在;
(Ⅲ)结合(Ⅱ),说明函数f(x)当k=2时为增函数,把不等式变形e
2x≥2x
2+2x+1=x
2+(x+1)
2后,依次取x的值为0,1,2…,(n-1),累加后利用等比数列求和公式可得结论.
点评:本题考查了利用导函数研究函数的单调性,考查了函数中的恒成立问题,考查了不等式的证明,解答此题的关键是运用导函数分析函数的单调性,同时考查了学生灵活的变式思维能力,此题属难题.

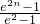 与
与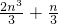 (n为任意非负整数)的大小关系,并给出证明.
(n为任意非负整数)的大小关系,并给出证明.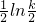 .
.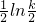 )上为减函数,而g(0)=0,所以,g(x)在[0,
)上为减函数,而g(0)=0,所以,g(x)在[0,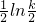 )上小于0.
)上小于0.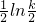 )上为减函数,而f(0)=0,故此时f(x)<0,不合题意.
)上为减函数,而f(0)=0,故此时f(x)<0,不合题意.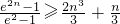 .
.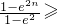
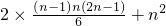 .
.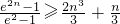 .
.

 阅读快车系列答案
阅读快车系列答案