Question

4．作出函数f（x）=$\left\{\begin{array}{l}{2-x，x＜1}\\{2{x}^{2}，x≥1}\end{array}\right.$ 的图形，并讨论它在x=1处极限是否存在．

Answer 1

分析 作出函数f（x）的图形，结合图形，计算$\underset{lim}{x{→1}^{-}}$f（x）与$\underset{lim}{x{→1}^{+}}$f（x）的值，
从而判断f（x）在x=1处的极限是否存在．

解答 解：作出函数f（x）=$\left\{\begin{array}{l}{2-x，x＜1}\\{2{x}^{2}，x≥1}\end{array}\right.$ 的图形，
如图所示；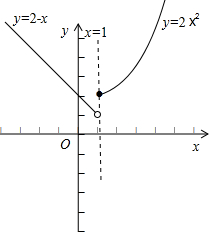
$\underset{lim}{x{→1}^{-}}$f（x）=2-1=1，
$\underset{lim}{x{→1}^{+}}$f（x）=2×1²=2，
$\underset{lim}{x{→1}^{-}}$f（x）≠$\underset{lim}{x{→1}^{+}}$f（x），
所以f（x）在x=1处的极限不存在．

点评 本题考查了函数在某一点处的极限是否存在的应用问题，是基础题．