
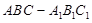 中,
中,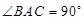 ,
,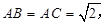
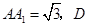 是
是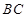 中点,
中点,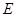 是
是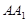 中点.
中点.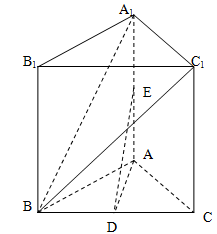
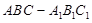 的体积;
的体积;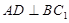 ;
;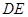 ∥面
∥面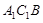 .
. ;(2)证明详见解析;(3)证明详见解析.
;(2)证明详见解析;(3)证明详见解析.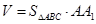 即可求解;(2)要证
即可求解;(2)要证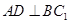 ,只须证明
,只须证明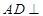 面
面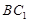 ,注意到面
,注意到面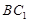 与底面
与底面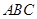 垂直且交线为
垂直且交线为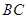 ,而依题意又有
,而依题意又有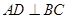 ,由面面垂直的性质可得
,由面面垂直的性质可得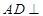 面
面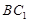 ,问题得证;(3)要证
,问题得证;(3)要证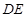 ∥面
∥面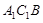 ,有两种思路:一是在平面
,有两种思路:一是在平面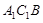 内找一条直线与
内找一条直线与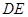 平行,这时只须取
平行,这时只须取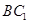 的中点
的中点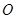 ,连接
,连接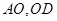 ,证明四边形
,证明四边形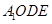 为平行四边形即可;二是先证经过直线
为平行四边形即可;二是先证经过直线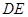 的一个平面与面
的一个平面与面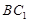 平行,这时可取
平行,这时可取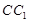 中点
中点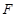 ,连结
,连结 ,
,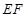 ,先证明面
,先证明面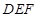 ∥面
∥面 ,再由面面平行的性质即可证明
,再由面面平行的性质即可证明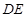 ∥面
∥面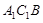 .
.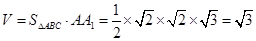 3分
3分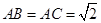 ,∴
,∴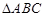 为等腰三角形
为等腰三角形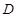 为
为 中点,∴
中点,∴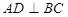 -4分
-4分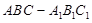 为直棱柱,∴面
为直棱柱,∴面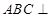 面
面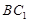 5分
5分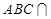 面
面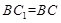 ,
,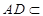 面
面
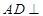 面
面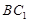 6分
6分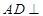
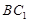 7分
7分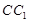 中点
中点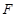 ,连结
,连结 ,
,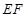 8分
8分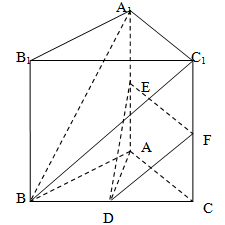
 分别为
分别为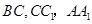 的中点
的中点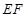 ∥
∥ ,
, ∥
∥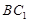 , 9分
, 9分
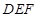 ∥面
∥面 11分
11分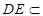 面
面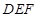
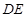 ∥面
∥面 12分.
12分.

科目:高中数学 来源:不详 题型:解答题
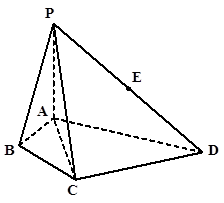
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.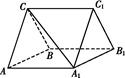
 ,求三棱柱ABC
,求三棱柱ABC A1B1C1的体积.
A1B1C1的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
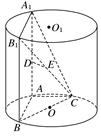
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
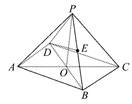
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,则此长方体的体积是________.
,则此长方体的体积是________.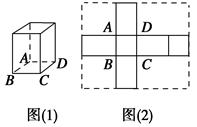
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com