
已知函数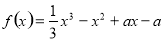 (
(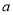
 R).
R).
(1)当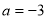 时,求函数
时,求函数 的极值;
的极值;
(2)若函数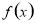 的图象与
的图象与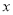 轴有且只有一个交点,求
轴有且只有一个交点,求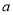 的取值范围.
的取值范围.
(1)当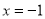 时,
时, 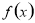 取得极大值为
取得极大值为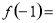
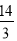 ;
;
当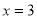 时,
时, 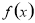 取得极小值为
取得极小值为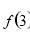
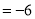 .
.
(2)a的取值范围是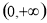 .
.
【解析】
试题分析:(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”.
(2)根据  =
= 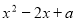 ,得到△=
,得到△= 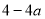 =
= 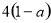 .
.
据此讨论:① 若a≥1,则△≤0,
此时 ≥0在R上恒成立,f(x)在R上单调递增 .
≥0在R上恒成立,f(x)在R上单调递增 .
计算f(0)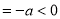 ,
,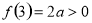 ,得到结论.
,得到结论.
② 若a<1,则△>0, = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为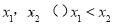 .
.
有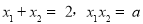 .
.
给出当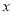 变化时,
变化时,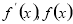 的取值情况表.
的取值情况表.
根据f(x1)·f(x2)>0, 解得a>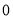 .作出结论.
.作出结论.
试题解析: (1)当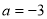 时,
时,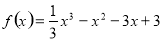 ,
,
∴
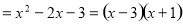 .
.
令 =0, 得
=0, 得  . 2分
. 2分
当 时,
时, , 则
, 则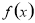 在
在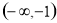 上单调递增;
上单调递增;
当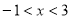 时,
时,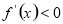 , 则
, 则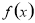 在
在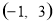 上单调递减;
上单调递减;
当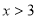 时,
时, ,
, 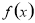 在
在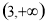 上单调递增. 4分
上单调递增. 4分
∴ 当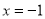 时,
时, 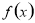 取得极大值为
取得极大值为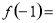
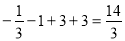 ;
;
当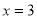 时,
时, 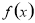 取得极小值为
取得极小值为
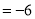 . 6分
. 6分
(2) ∵  =
= 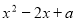 ,
,
∴△= 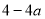 =
= 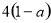 .
.
① 若a≥1,则△≤0, 7分
∴ ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0)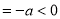 ,
,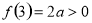 ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. 9分
② 若a<1,则△>0,
∴ = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为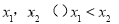 .
.
∴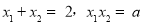 .
.
当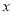 变化时,
变化时,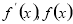 的取值情况如下表:
的取值情况如下表:
x |
| x1 | (x1,x2) | x2 |
|
| + | 0 | - | 0 | + |
f(x) | ↗ | 极大值
| ↘ | 极小值
| ↗ |
11分
∵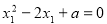 ,
,
∴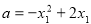 .
.
∴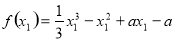
=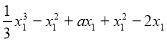
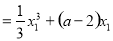
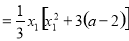 .
.
同理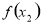
 .
.
∴
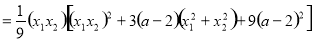
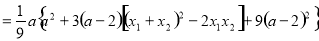
 .
.
令f(x1)·f(x2)>0, 解得a>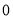 .
.
而当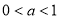 时,
时,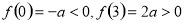 , 13分
, 13分
故当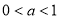 时, 函数f(x)的图象与x轴有且只有一个交点.
时, 函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是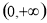 . 14分
. 14分
考点:应用导数研究函数的极值、单调性及函数的图象,分类讨论思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年安徽省“江南十校”高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
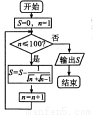
执行如图所示的程序框图,输出的 是( )
是( )
A.9 B.10 C.-9 D.-10
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知某程序框图如图所示,则该程序运行后输出的结果为( )

A.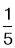 B.
B.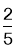 C.
C. D.
D.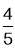
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市高三5月文科数学试卷(解析版) 题型:选择题
对任意实数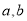 ,记
,记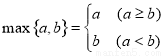 ,若
,若 ,其中奇函数
,其中奇函数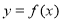 在
在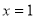 时有极小值
时有极小值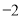 ,
, 是正比例函数,
是正比例函数,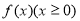 与
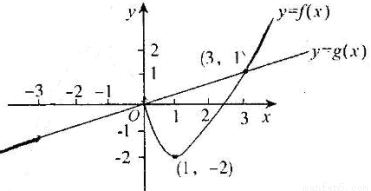
与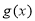 图象如图,则下列关于
图象如图,则下列关于 的说法中正确的是( )
的说法中正确的是( )
A.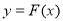 是奇函数
是奇函数
B.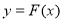 有极大值
有极大值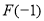 和极小值
和极小值
C.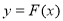 的最小值为
的最小值为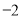 ,最大值为2
,最大值为2
D.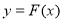 在
在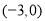 上是增函数
上是增函数
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市高考5月模拟理科数学试卷(解析版) 题型:填空题
已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市红桥区高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
某选修课的考试按A级、B级依次进行,只有当A级成绩合格时,才可继续参加B级的考试.已知每级考试允许有一次补考机会,两个级别的成绩均合格方可获得该选修课的合格证书.现某人参加这个选修课的考试,他A级考试成绩合格的概率为 ,B级考试合格的概率为
,B级考试合格的概率为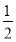 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得该选修课的合格证书的概率;
(2)在这个考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为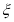 ,求
,求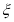 的数学期望E
的数学期望E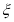 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com