练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体中，为棱、的三等分点（靠近A点）.

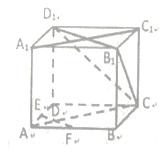
    求证：（1）平面；

    （2）求证：平面平面.

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）欲证：平面，根据直线与平面平行的判定定理可知，只需证与平面内一条直线平行，连接，可知，则，又平面，平面，满足定理所需条件；

    （2）欲证：平面平面，根据面面垂直的判定定理可知，在平面内一条直线与平面垂直，而平面，平面，则，，满足线面垂直的判定定理则平面，而平面，满足定理所需条件．

    （1）证明：连接，在正方体中，对角线，

    又因为、为棱、的三等分点，

    所以，则，

    又平面，平面，

    所以平面．

    （2）因为在正方体中，

    因为平面，而平面，

    所以，

    又因为在正方形中，，

    而，

    平面，平面，

    所以平面，

    又因为平面，

    所以平面平面．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“砥砺奋进的五年”，首都经济社会发展取得新成就.自2012年以来，北京城乡居民收入稳步增长.随着扩大内需，促进消费等政策的出台，居民消费支出全面增长，消费结构持续优化升级，城乡居民人均可支配收入快速增长，人民生活品质不断提升.下图是北京市2012-2016年城乡居民人均可支配收入实际增速趋势图（例如2012年，北京城镇居民收入实际增速为7.3%，农村居民收入实际增速为8.2%）.

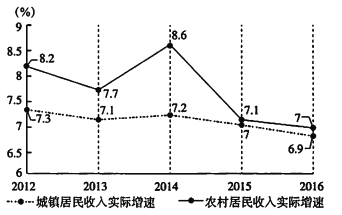
    （Ⅰ）从2012-2016五年中任选一年，求城镇居民收入实际增速大于7%的概率；

    （Ⅱ）从2012-2016五年中任选一年，求至少有一年农村和城镇居民收入实际增速均超过7%的概率；

    （Ⅲ）由图判断，从哪年开始连续三年农村居民收入实际增速方差最大？（结论不要求证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左焦点为，离心率．

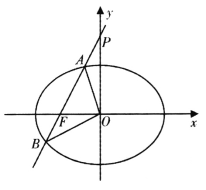
    (I)求椭圆C的标准方程；

    (II)已知直线交椭圆C于A，B两点．

    ①若直线经过椭圆C的左焦点F，交y轴于点P，且满足.求证：为定值；

    ②若，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知圆与轴的左右交点分别为，与轴正半轴的交点为.

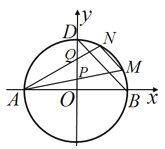
    （1）若直线过点并且与圆相切，求直线的方程；

    （2）若点是圆上第一象限内的点，直线分别与轴交于点，点是线段的中点，直线，求直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，直线与E交于A、B两点，且，其中O为原点.

    （1）求抛物线E的方程；

    （2）点C坐标为，记直线CA、CB的斜率分别为，证明： 为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：（）的离心率为，短轴端点到焦点的距离为.

    （1）求椭圆的方程；

    （2）设，为椭圆上任意两点，为坐标原点，且.求证：原点到直线的距离为定值，并求出该定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为函数的导函数，且.

    （1）判断函数的单调性；

    （2）若，讨论函数零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知(b－c)2＝a2－bc.

    (1)求sinA；

    (2)若a＝2，且sinB，sinA，sinC成等差数列，求△ABC的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝x3﹣x2+x，a∈R．

    （Ⅰ）当a＝1时，求f（x）在[﹣1，1]上的最大值和最小值；

    （Ⅱ）若f（x）在区间[，2]上单调递增，求a的取值范围；

    （Ⅲ）当m＜0时，试判断函数g（x）＝-其中f′（x）是f（x）的导函数）是否存在零点，并说明理由．

    查看答案和解析>>

    同步练习册答案