
【题目】已知函数f(x)=![]() x3﹣
x3﹣![]() x2+x,a∈R.
x2+x,a∈R.
(Ⅰ)当a=1时,求f(x)在[﹣1,1]上的最大值和最小值;
(Ⅱ)若f(x)在区间[![]() ,2]上单调递增,求a的取值范围;
,2]上单调递增,求a的取值范围;
(Ⅲ)当m<0时,试判断函数g(x)=![]() -
-![]() 其中f′(x)是f(x)的导函数)是否存在零点,并说明理由.
其中f′(x)是f(x)的导函数)是否存在零点,并说明理由.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)求出![]() ,对
,对![]() 的正负判断,从而确定函数的单调性,即可求得函数的最值。
的正负判断,从而确定函数的单调性,即可求得函数的最值。
(Ⅱ)转化成![]() 在区间[
在区间[![]() ,2]恒成立,再参变分离,转化成函数最值问题,利用基本不等式求最值即可。
,2]恒成立,再参变分离,转化成函数最值问题,利用基本不等式求最值即可。
(Ⅲ)将所求问题化简转化成方程![]() 在
在![]() 内是否有解,利用导数说明函数
内是否有解,利用导数说明函数![]() 的单调性,再由
的单调性,再由![]() 即可判断原函数不存在零点。
即可判断原函数不存在零点。
(Ⅰ)当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() 得
得![]() 或
或![]() .
.
当x变化时,![]() ,f(x)的变化情况如下表:
,f(x)的变化情况如下表:
x |
|
|
|
|
|
| + | 0 |
| ||
f(x) |
| 单调递增↗ | 极大值 | 单调递减↘ |
|
∴![]() ,
,
![]() .
.
(Ⅱ)![]()
∵![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,
∴![]() 在
在![]() 上恒成立.
上恒成立.
即:![]() .
.
∵![]() ,
,
∴当且仅当![]() 时,
时,![]() 成立.
成立.
∴![]()
(Ⅲ)由题意可知,![]() ,
, ![]()
要判断![]() 是否存在零点,只需判断方程
是否存在零点,只需判断方程![]() 在
在![]() 内是否有解,
内是否有解,
即要判断方程![]() 在
在![]() 内是否有解.
内是否有解.
设![]() ,
,
![]()
![]() ,
,
可见,当![]() 时,
时,![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减.
上单调递减.
∵![]() ,
,
∴![]() 在
在![]() 和
和![]() 内均无零点。
内均无零点。
故函数g(x)=![]() -
-![]() 无零点
无零点


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】如图,为方便金湖县人民游览三河风景区附近的“网红桥”,现准备在河岸一侧建造一个观景台A,已知射线PM, PN为两边夹角为120°的公路(长度均超过5千米),在两条公路PM,PN上分别设立游客上下点B、C,在观景台A和游客上下点B、C之间和游客上下点B、C之间分别建造三条观光线路AB,AC,BC,测得PB=3干米,PC=5千米.

(1)求线段BC的长度;
(2)若∠BAC= 60°,因政府要计算修建三条观光线路所需费用,所以要计算AB,AC,BC三条线路的总长度的取值范围,请你建立合适的数学模型,帮助政府解决这个问题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-x2)ex-1.
(1)求函数f(x)的单调区间;
(2)若对任意x≥1,都有f(x)-mx-1+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )
A. 若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,则
,则![]()
C. 若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市创业园区新引进一家生产环保产品的公司,已知该环保产品每售出1盒的利润为0.3万元,当月未售出的环保产品,每盒亏损0.12万元.根据统计资料,该环保产品的市场月需求量的频率分布直方图如图所示.
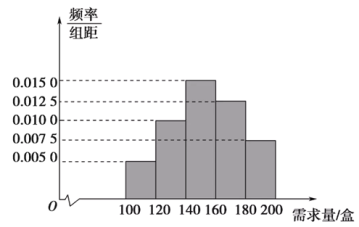
(1)若该环保产品的月进货量为160盒,以![]() (单位:盒,
(单位:盒,![]() )表示该产品一个月内的市场需求量,
)表示该产品一个月内的市场需求量,![]() (单位:万元)表示该公司生产该环保产品的月利润.
(单位:万元)表示该公司生产该环保产品的月利润.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②根据频率分布直方图估计利润![]() 不少于39.6万元的概率.
不少于39.6万元的概率.
(2)在频率分布直方图的月需求量分组中,以各组的区间中点值代表该组的月需求量,当月进货量为158箱时,写出月利润![]() (单位:万元)的所有可能值.
(单位:万元)的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com