
����Ŀ��ij�д�ҵ��������һ������������Ʒ�Ĺ�˾����֪�û�����Ʒÿ�۳�1�е�����Ϊ0.3��Ԫ������δ�۳��Ļ�����Ʒ��ÿ�п���0.12��Ԫ������ͳ�����ϣ��û�����Ʒ���г�����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
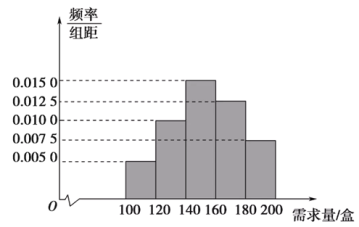
��1�����û�����Ʒ���½�����Ϊ160�У���![]() ����λ���У�
����λ���У�![]() ����ʾ�ò�Ʒһ�����ڵ��г���������
����ʾ�ò�Ʒһ�����ڵ��г���������![]() ����λ����Ԫ����ʾ�ù�˾�����û�����Ʒ��������
����λ����Ԫ����ʾ�ù�˾�����û�����Ʒ��������
�ٽ�![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
�ڸ���Ƶ�ʷֲ�ֱ��ͼ��������![]() ������39.6��Ԫ�ĸ��ʣ�
������39.6��Ԫ�ĸ��ʣ�
��2����Ƶ�ʷֲ�ֱ��ͼ���������������У��Ը���������е�ֵ����������������������½�����Ϊ158��ʱ��д��������![]() ����λ����Ԫ�������п���ֵ��
����λ����Ԫ�������п���ֵ��
���𰸡���1����![]() ����0.7����2�����п���ֵΪ27.24��Ԫ��35.64��Ԫ��44.04��Ԫ��47.4��Ԫ��
����0.7����2�����п���ֵΪ27.24��Ԫ��35.64��Ԫ��44.04��Ԫ��47.4��Ԫ��
��������
��1���ٸ��ݷֶκ����ı���ʽ�����ɽ�![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
�ڸ���ֱ��ͼ���![]() ������
������![]() ��Ԫȡֵ��Χ�����ɵõ����ۣ�
��Ԫȡֵ��Χ�����ɵõ����ۣ�
��3������������Ϊ![]() ����
����![]() �����п��ܵ�ֵΪ110��130��150��170��190���ֱ������Ӧ��
�����п��ܵ�ֵΪ110��130��150��170��190���ֱ������Ӧ��![]() ��ֵ��
��ֵ��
��1���ٵ�![]() ʱ��
ʱ��
![]()
![]()
��![]() ʱ��
ʱ��![]()
![]() ��
��
�ڡ���������39.6��Ԫ
�൱![]() ʱ��
ʱ��![]()
![]()
�ֵ�![]() ʱ��
ʱ��![]()
�൱![]() ʱ��
ʱ��![]()
��Ƶ�ʷֲ�ֱ��ͼ��֪��![]() ��Ƶ��Ϊ
��Ƶ��Ϊ
![]()
������![]() ������39.6��Ԫ�ĸ���Ϊ0.7��
������39.6��Ԫ�ĸ���Ϊ0.7��
��2������������Ϊ![]() ����
����![]() �����п��ܵ�ֵΪ110��130��150��170��190
�����п��ܵ�ֵΪ110��130��150��170��190
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
��![]() ʱ��
ʱ��![]()
���Ͽ�֪��![]() �����п���ֵΪ27.24��Ԫ��35.64��Ԫ��44.04��Ԫ��47.4��Ԫ��
�����п���ֵΪ27.24��Ԫ��35.64��Ԫ��44.04��Ԫ��47.4��Ԫ��


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����![]() x3��
x3��![]() x2+x��a��R��
x2+x��a��R��
����a��1ʱ����f��x����[��1��1]�ϵ����ֵ����Сֵ��
������f��x��������[![]() ��2]�ϵ�����������a��ȡֵ��Χ��
��2]�ϵ�����������a��ȡֵ��Χ��
����m��0ʱ�����жϺ���g��x����![]() -
-![]() ����f�䣨x����f��x���ĵ��������Ƿ������㣬��˵�����ɣ�
����f�䣨x����f��x���ĵ��������Ƿ������㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������
��������![]() ,
,![]() ����Բ��.
����Բ��.
��1������Բ![]() �ı�����;
�ı�����;
��2����֪��ֱ��![]() ��б�ʴ��ڣ�����Բ�ཻ�ڵ�
��б�ʴ��ڣ�����Բ�ཻ�ڵ�![]() ����,��
����,��![]() �����
�����![]() ,��
,��![]() Ϊ�߶�
Ϊ�߶�![]() ���е�.
���е�.![]() ����
����![]() ����ͶӰΪ
����ͶӰΪ![]() ,�ʣ���
,�ʣ���![]() �����Ƿ������������
�����Ƿ������������![]() ,ʹ��
,ʹ��![]() Ϊ��ֵ,���������
Ϊ��ֵ,���������![]() ������;��������,��˵������.
������;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �Ķ���������ԭ�㣬������x���ϣ��ҹ���(2��4)��Բ
�Ķ���������ԭ�㣬������x���ϣ��ҹ���(2��4)��Բ![]() ����Բ��
����Բ��![]() ��ֱ��l�������ߺ�Բ�ֱ���P��Q��M��N����
��ֱ��l�������ߺ�Բ�ֱ���P��Q��M��N����![]() ����СֵΪ________��
����СֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
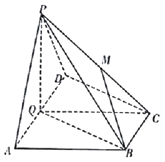
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊֱ�����Σ�
Ϊֱ�����Σ� ![]() ��
�� ![]() ��ƽ��
��ƽ��![]() ����
����![]() ��
�� ![]() Ϊ
Ϊ![]() ���е㣬
���е㣬 ![]() ����
����![]() �ϵĵ㣬
�ϵĵ㣬 ![]() ��
�� ![]() ��
�� ![]() .
.
������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
����������ֱ��![]() ��
��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���˲���
���˲���![]() ����ְͨ���������룬����
����ְͨ���������룬����![]() �����ݵ���λ��Ϊ
�����ݵ���λ��Ϊ![]() ��ƽ����Ϊ
��ƽ����Ϊ![]() ������Ϊ
������Ϊ![]() ������ټ�����������������
������ټ�����������������![]() ������
������![]() �������У�����˵����ȷ���ǣ� ��
�������У�����˵����ȷ���ǣ� ��
A. ������ƽ�������ܲ��䣬��λ�����ܲ��䣬������ܲ���
B. ������ƽ�������������λ�����ܲ��䣬������
C. ������ƽ�������������λ�����ܲ��䣬����Ҳ����
D. ������ƽ�������������λ��һ���������ܲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��2���Ƿ����ʵ��![]() ��ʹ��������һ��
��ʹ��������һ��![]() ��ʹ
��ʹ![]() �����������ڣ����ʵ��
�����������ڣ����ʵ��![]() ��ȡֵ��Χ���������ڣ�˵������.
��ȡֵ��Χ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() ����
����![]() ����
����![]() ʱ����
ʱ����![]() ������
������
��1���ж�![]() ��
��![]() �ϵĵ����ԣ�������֤����
�ϵĵ����ԣ�������֤����
��2����![]() �������
�������![]() �Լ�����
�Լ�����![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ��
��
��1����ʵ��![]() ��ֵ��
��ֵ��
��2���жϺ���![]() ������
������![]() �ϵĵ����ԣ����ú��������ԵĶ���֤����
�ϵĵ����ԣ����ú��������ԵĶ���֤����
��3����ʵ��![]() ��ȡֵ��Χ��ʹ�ù���
��ȡֵ��Χ��ʹ�ù���![]() �ķ���
�ķ���![]() �ֱ�Ϊ��
�ֱ�Ϊ��
�����ҽ���һ��ʵ���⣻����������ͬ��ʵ���⣻����������ͬ��ʵ���⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com