
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)函数![]() 在
在![]() 上的最大值
上的最大值![]() .
.
①求![]() ;
;
②若过点![]() 可作出曲线
可作出曲线![]() 的三条切线,求
的三条切线,求![]() 的范围.
的范围.
【答案】(1)见解析;(2)①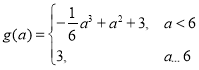 ;②
;②![]() 或
或![]() 且
且![]() .
.
【解析】
(1)求![]() ,令
,令![]() 便得到
便得到![]() ,或
,或![]() ,所以讨论
,所以讨论![]() 和2的关系,即判断
和2的关系,即判断![]() 和0的关系:分
和0的关系:分![]() ,
,![]() ,
,![]() 三种情况,判断每种情况下的
三种情况,判断每种情况下的![]() 的符号,从而判断
的符号,从而判断![]() 的单调性;
的单调性;
(2)①对应(1)中的三种情况:![]() ,
,![]() ,
,![]() ,判断在每种情况下
,判断在每种情况下![]() 在
在![]() ,
,![]() 上的单调性,根据单调性求函数
上的单调性,根据单调性求函数![]() 在
在![]() ,
,![]() 上的最大值
上的最大值![]() ;
;
②要作![]() 的三条切线,则
的三条切线,则![]() 图象应是曲线,所以
图象应是曲线,所以![]() ,
,![]() ,求
,求![]() ,设切点为
,设切点为![]() ,将切点
,将切点![]() 代入切线方程,则这个关于
代入切线方程,则这个关于![]() 的方程有三个不同的实数根,再利用导数研究三次方程根的情况,即可求得
的方程有三个不同的实数根,再利用导数研究三次方程根的情况,即可求得![]() 的取值范围.
的取值范围.
(1)![]() ,令
,令![]() 得,
得,![]() ,或
,或![]() ;
;
若![]() ,即
,即![]() ,
,
![]() ,或
,或![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;
上单调递减;
若![]() ,即
,即![]() ,
,![]() ,
,
![]() 函数
函数![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,
,![]() ,
,![]() ,或
,或![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 单调递减;
单调递减;
(2)①由(1)知:
![]() 当
当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() ,
,![]() 单调递增;
单调递增;
![]() 对于此时的
对于此时的![]() 的最大值比较
的最大值比较![]() ,
,![]() 即可;
即可;
∵![]() ,
,
![]() 时,
时,![]() ,∴
,∴![]() ;
;
∵![]() 时,
时,![]() ,∴
,∴![]() ;
;
![]() 当
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,∴
上单调递增,∴![]() ;
;
![]() 当
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,∴
上单调递增,∴![]() ;
;
∴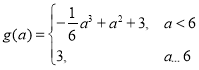 ;
;
②根据题意,![]() ,
,![]() ,
,
所以设过点![]() 所作切线的切点为
所作切线的切点为![]() ,
,![]() ,斜率为
,斜率为![]() ;
;
![]() 切线方程为
切线方程为![]() ,
,
∵点![]() 在切线上,所以
在切线上,所以![]() ,
,
将上式整理成:![]() ,
,
则关于![]() 的方程有三个不同的实数根,且
的方程有三个不同的实数根,且![]() ;
;
令![]() ,
,
则![]() 应有三个不同的零点,
应有三个不同的零点,![]() ,令
,令![]() ,则
,则![]() ,或
,或![]() ,
,![]() ,
,![]() 中一个是极大值,一个是极小值;
中一个是极大值,一个是极小值;
![]() 时,
时,![]() 是极小值,
是极小值,![]() 是极大值,
是极大值,![]()
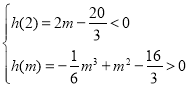 ;
;
解![]() 得
得![]() ;
;
令![]() ,
,![]() ,令
,令![]() ,得,
,得,![]() ,或4;
,或4;
![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
可求得![]() ,
,![]() ,时,
,时,![]() ,
,![]() ,且
,且![]() 时,
时,![]() ;
;
![]() 的解是
的解是![]() ,
,![]() ;
;
![]() 时,
时,![]() 是极大值,
是极大值,![]() 是极小值,
是极小值,![]()
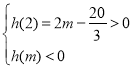 ;
;
解![]() 得,
得,![]() ;
;
∴![]() 的解是
的解是![]() ,且
,且![]() ,
,![]() ,且
,且![]() ;
;
综上得![]() 的取值范围是
的取值范围是![]() 或
或![]() 且
且![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点和上顶点的直线与圆
的左焦点和上顶点的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 与原点
与原点![]() 关于直线
关于直线![]() 对称,试求四边形
对称,试求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别是a,b,c,且csin2B﹣bsin(A+B)=0
(1)求角B的大小;
(2)设a=4,c=6,求sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数
个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数![]() 的图象,对于函数
的图象,对于函数![]() 有以下四个判断:
有以下四个判断:
①该函数的解析式为;![]() ;
;
②该函数图象关于点![]() 对称;
对称;
③该函数在![]() [,上是增函数;
[,上是增函数;
④函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,则
,则![]() .
.
其中,正确判断的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 、
、![]() ,对于给定的正整数
,对于给定的正整数![]() ,记
,记![]() ,
,![]()
![]() .若对任意的正整数
.若对任意的正整数![]() 满足:
满足:![]() ,且
,且![]() 是等差数列,则称数列
是等差数列,则称数列![]() 为“
为“![]() ”数列.
”数列.
(1)若数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() 为
为![]() 数列;
数列;
(2)若数列![]() 为
为![]() 数列,且
数列,且![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若数列![]() 为
为![]() 数列,证明:
数列,证明:![]() 是等差数列 .
是等差数列 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的
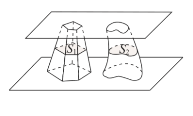
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,记
,记![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)① 计算![]() ,
,![]() 的值;
的值;
② 猜想![]() ,
,![]() 满足的关系式,并用数学归纳法加以证明;
满足的关系式,并用数学归纳法加以证明;
(2)若数列![]() 通项公式为
通项公式为![]() ,证明:
,证明:![]() .
.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com