
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点和上顶点的直线与圆
的左焦点和上顶点的直线与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 与原点
与原点![]() 关于直线
关于直线![]() 对称,试求四边形
对称,试求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)由题得:过椭圆![]() 的左焦点和上顶点的直线方程为
的左焦点和上顶点的直线方程为![]() ,又由该直线与圆相切得到:
,又由该直线与圆相切得到:![]() ,联立
,联立![]() ,解方程组即得;
,解方程组即得;
(2)由题得直线![]() 的斜率
的斜率![]() 一定存在,可设直线
一定存在,可设直线![]() ,代入椭圆方程,消元化简得:
,代入椭圆方程,消元化简得:
![]() ,由弦长公式求得
,由弦长公式求得![]() ,再求出点
,再求出点![]() 到直线
到直线![]() 的距离
的距离![]() ,算出
,算出![]() ,最后求出四边形
,最后求出四边形![]() 的面积的最大值.
的面积的最大值.
(1)过椭圆![]() 的左焦点和上顶点的直线方程为
的左焦点和上顶点的直线方程为![]() ,即
,即![]() ,
,
又该直线与圆![]() 相切,
相切,![]() ,又离心率
,又离心率![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)由点![]() 与原点
与原点![]() 关于直线
关于直线![]() 对称,得
对称,得![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴,四边形
轴,四边形![]() 不存在,不合题意.
不存在,不合题意.
当直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则直线
,则直线![]() ,设
,设![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
从而![]()
![]()
![]() ,
,
又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,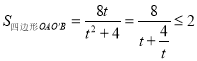 ,
,
当且仅当![]() ,即
,即![]() 时等号成立,且满足
时等号成立,且满足![]() ,
,
![]() 四边形
四边形![]() 的面积的最大值为2.
的面积的最大值为2.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:![]() ,当
,当![]() 且
且![]() 时,
时,![]() 且
且![]() ,其中
,其中![]() 均为非零常数.
均为非零常数.
(1)数列![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)令![]() ,若
,若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)证明:![]() 数列是等比数列的充要条件是
数列是等比数列的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | 10 | 10 |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值
元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为
元的奖品.已知中奖率为![]() ,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为
,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量比去年同期增长
.若今年国庆期间该商场的购物单数量比去年同期增长![]() ,式预测商场今年国庆期间采办奖品的开销.
,式预测商场今年国庆期间采办奖品的开销.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2018年1月至12月石油进口量统计图(其中同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比),则下列说法错误的是( )
个月之比),则下列说法错误的是( )
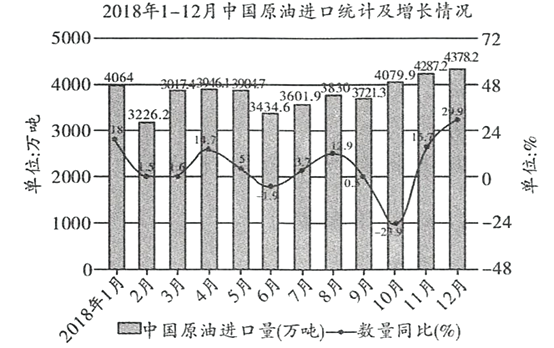
A.2018年下半年我国原油进口总量高于2018年上半年
B.2018年12个月中我国原油月最高进口量比月最低进口量高1152万吨
C.2018年我国原油进口总量高于2017年我国原油进口总量
D.2018年1月—5月各月与2017年同期相比较,我国原油进口量有增有减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 位萌娃参加一项“寻宝贝,互助行”的游戏活动,宝贝的藏匿地点有远、近两处,其中亮亮的年龄比较小,要么不参与此项活动,但同时必须有另--位萌娃留下陪同;要么参与寻找近处的宝贝.所有参与寻找宝贝任务的萌娃被平均分成两组,一组去远处,一组去近处,那么不同的寻找方案有( )
位萌娃参加一项“寻宝贝,互助行”的游戏活动,宝贝的藏匿地点有远、近两处,其中亮亮的年龄比较小,要么不参与此项活动,但同时必须有另--位萌娃留下陪同;要么参与寻找近处的宝贝.所有参与寻找宝贝任务的萌娃被平均分成两组,一组去远处,一组去近处,那么不同的寻找方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,经过点
,经过点![]() 的直线与抛物线
的直线与抛物线![]() 交于不同的
交于不同的![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,经过点
,经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求抛物线![]() 的方程和焦点
的方程和焦点![]() 的坐标;
的坐标;
(2)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中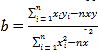 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com