练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现有位萌娃参加一项“寻宝贝，互助行”的游戏活动，宝贝的藏匿地点有远、近两处，其中亮亮的年龄比较小，要么不参与此项活动，但同时必须有另--位萌娃留下陪同；要么参与寻找近处的宝贝.所有参与寻找宝贝任务的萌娃被平均分成两组，一组去远处，一组去近处，那么不同的寻找方案有（ ）

    A.种B.种C.种D.种

    【答案】B

    【解析】

    按照亮亮参与，不参与游戏分类讨论，即可求出所有的寻找方案．

    (1)若亮亮不参与游戏，可以分三步完成萌娃的分配：①安排一位萌娃陪同亮亮，有5种选择：②从剩下的4个萌娃选择2个去近处，有种选择；③最后剩下的2个去远处，完成分配，所以有种方案．

    (2)若亮亮参与游戏，可以分两步完成萌娃的分配：①从5个萌娃选择2个和亮亮去近处，有种选择；②剩下的3个萌娃去远处，完成分配，所以有种方案．

    综上，不同的寻找方案有种．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，平面平面，四边形和都是边长为2的正方形，点，分别是，的中点，二面角的大小为60°.

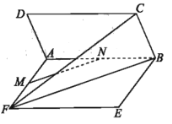
    （1）求证：平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，直线的斜率为，直线的斜率为，且.

    （1）求点的轨迹的方程；

    （2）设，，连接并延长，与轨迹交于另一点，点是中点，是坐标原点，记与的面积之和为，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）讨论函数的极值;

    （2）若为整数,,且,不等式成立，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆（）的离心率为，过椭圆的左焦点和上顶点的直线与圆相切.

    （1）求椭圆的方程；

    （2）过点的直线与椭圆交于、两点，点与原点关于直线对称，试求四边形的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆的参数方程为(其中为参数)，以原点为极点，轴非负半轴为极轴建立极坐标系，则曲线的极坐标方程为.

    （1）求圆的普通方程与的直角坐标方程；

    （2）点是曲线上一点，由向圆引切线，切点分别为，求四边形面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，是的中点，.

    （1）求证：平面；

    （2）若异面直线和所成角的余弦值为，求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=lnx+ax2+(2a+1)x．

    （1）讨论的单调性；

    （2）当a﹤0时，证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的导函数为.

    （1）若对任意恒成立，求实数的取值范围；

    （2）若函数的极值为正数，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案