
| 2a2 |
| x |
| 2x2-2a2 |
| x |
| 2(x+a)(x-a) |
| x |
| x | (0,a) | a | (a,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
| ||
| 2 |
| e |
| e |
| e |


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
. |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
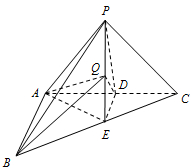 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2| 3 |
| 2 |
| QE |
| PE |
查看答案和解析>>
科目:高中数学 来源: 题型:
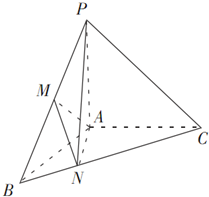 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| e |
| e-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com