
用数学归纳法证明1+2+3+…+(3n+1)=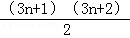 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.(3k+2)
B.(3k+4)
C.(3k+2)+(3k+3)
D.(3k+2)+(3k+3)+(3k+4)
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例(解析版) 题型:解答题
试比较nn+1与(n+1)n(n∈N*)的大小.
当n=1时,有nn+1 (n+1)n(填>、=或<);
当n=2时,有nn+1 (n+1)n(填>、=或<);
当n=3时,有nn+1 (n+1)n(填>、=或<);
当n=4时,有nn+1 (n+1)n(填>、=或<);
猜想一个一般性的结论,并加以证明.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证“1﹣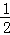 +
+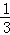 ﹣
﹣ +…+
+…+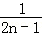 ﹣
﹣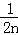 =
=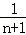 +
+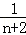 +…+
+…+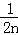 (n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
(n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
A.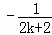 B.
B.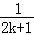 C.
C.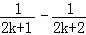 D.
D.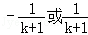
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明:1+2+22+…2n﹣1=2n﹣1(n∈N)的过程中,第二步假设当n=k时等式成立,则当n=k+1时应得到( )
A.1+2+22+…+2k﹣2+2k+1﹣1
B.1+2+22+…+2k+2k+1=2k﹣1+2k+1
C.1+2+22+…+2k﹣1+2k+1=2k+1﹣1
D.1+2+22+…+2k﹣1+2k=2k﹣1+2k
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷(解析版) 题型:解答题
设正整数构成的数列{an}使得a10k﹣9+a10k﹣8+…+a10k≤19对一切k∈N*恒成立.记该数列若干连续项的和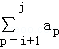 为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷(解析版) 题型:选择题
若a<b<c,x<y<z,则下列各式中值最大的一个是( )
A.ax+cy+bz B.bx+ay+cz
C.bx+cy+az D.ax+by+cz
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷(解析版) 题型:选择题
下面叙述正确的是( )
A.综合法、分析法是直接证明的方法
B.综合法是直接证法、分析法是间接证法
C.综合法、分析法所用语气都是肯定的
D.综合法、分析法所用语气都是假定的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com