
试比较nn+1与(n+1)n(n∈N*)的大小.
当n=1时,有nn+1 (n+1)n(填>、=或<);
当n=2时,有nn+1 (n+1)n(填>、=或<);
当n=3时,有nn+1 (n+1)n(填>、=或<);
当n=4时,有nn+1 (n+1)n(填>、=或<);
猜想一个一般性的结论,并加以证明.
<,<,>,>
【解析】
试题分析:本题考查的知识点是归纳推理与数学归纳法,我们可以列出nn+1与(n+1)n(n∈N*)的前若干项,然后分别比较其大小,然后由归纳推理猜想出一个一般性的结论,然后利用数学归纳法进行证明.
【解析】
当n=1时,nn+1=1,(n+1)n=2,此时,nn+1<(n+1)n,
当n=2时,nn+1=8,(n+1)n=9,此时,nn+1<(n+1)n,
当n=3时,nn+1=81,(n+1)n=64,此时,nn+1>(n+1)n,
当n=4时,nn+1=1024,(n+1)n=625,此时,nn+1>(n+1)n,
根据上述结论,我们猜想:当n≥3时,nn+1>(n+1)n(n∈N*)恒成立.
①当n=3时,nn+1=34=81>(n+1)n=43=64
即nn+1>(n+1)n成立.
②假设当n=k时,kk+1>(k+1)k成立,即: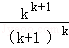 >1
>1
则当n=k+1时,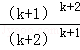 =
=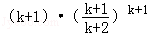 >
>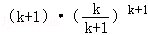 =
=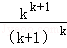 >1
>1
即(k+1)k+2>(k+2)k+1成立,即当n=k+1时也成立,
∴当n≥3时,nn+1>(n+1)n(n∈N*)恒成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.6弃九验算法练习卷(解析版) 题型:选择题
(2014•沈阳模拟)用“秦九韶”算法计算多项式f(x)=5x5+4x4+3x3+2x2+x+1当x=2时的值时,需要做乘法和加法的次数分别为( )
A.4,4 B.4,5 C.5,4 D.5,5
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型:选择题
利用更相减损术求99,36的最大公约数的操作步骤为(99,36)→(63,36)→(27,36)→(27,9)→(18,9)→(9,9),那么99,36的最大公约数为( )
A.36 B.27 C.18 D.9
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
把88化为五进制数是( )
A.324(5) B.323(5) C.233(5) D.332(5)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
下列各数中最小的数是( )
A.85(9) B.210(6) C.1000(4) D.11111(2)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例(解析版) 题型:解答题
(2008•武汉模拟)在数列|an|中,a1=t﹣1,其中t>0且t≠1,且满足关系式:an+1(an+tn﹣1)=an(tn+1﹣1),(n∈N+)
(1)猜想出数列|an|的通项公式并用数学归纳法证明之;
(2)求证:an+1>an,(n∈N+).
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例(解析版) 题型:选择题
用数学归纳法证明不等式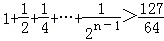 成立,起始值至少应取为( )
成立,起始值至少应取为( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明1+2+3+…+(3n+1)=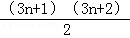 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.(3k+2)
B.(3k+4)
C.(3k+2)+(3k+3)
D.(3k+2)+(3k+3)+(3k+4)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷(解析版) 题型:选择题
(2014•孝感二模)已知x,y,z均为正数,且x+y+z=2,则 +
+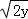 +
+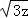 的最大值是( )
的最大值是( )
A.2 B.2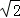 C.2
C.2 D.?3
D.?3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com