Question

5．在平面几何中，有“若△ABC的周长c，面积为S，则内切圆半径r=$\frac{2S}{c}$”，类比上述结论，在立体几何中，有“若四面体ABCD的表面积为S，体积为V，则其内切球的半径r=（　　）

• A． $\frac{3V}{S}$
• B． $\frac{2V}{S}$
• C． $\frac{V}{2S}$
• D． $\frac{V}{3S}$

Answer 1

分析 根据平面与空间之间的类比推理，由点类比点或直线，由直线 类比 直线或平面，由内切圆类比内切球，由平面图形面积类比立体图形的体积，结合求三角形的面积的方法类比求四面体的体积即可．

解答 解：设四面体的内切球的球心为O，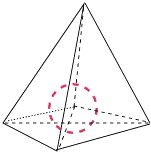
则球心O到四个面的距离都是R，
所以四面体的体积等于以O为顶点，
分别以四个面为底面的4个三棱锥体积的和．
则四面体的体积为 V四面体A-BCD=$\frac{1}{3}$（S₁+S₂+S₃+S₄）R
∴R=$\frac{3V}{S}$．
故选：A．

点评 本题考查类比推理的应用，类比推理是指依据两类数学对象的相似性，将已知的一类数学对象的性质类比迁移到另一类数学对象上去．一般步骤：①找出两类事物之间的相似性或者一致性．②用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（或猜想）．