
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
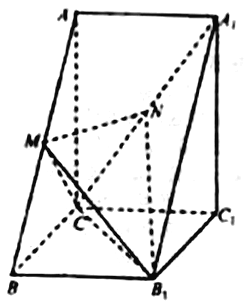
(1)求证: ![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题(1)连接![]() ,
, ![]() , 设法证明
, 设法证明![]() ,即可得到
,即可得到![]() 平面
平面![]() ;
;
(2)由![]() 平面
平面![]() ,得
,得![]() ,
, ![]() .
.
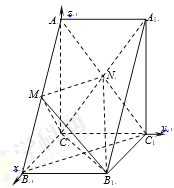
以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
求出相关点的坐标,得到直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,利用
的法向量,利用![]() 即可求出直线
即可求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:
(1)连接![]() ,
, ![]() ,则
,则![]() 且
且![]() 为
为![]() 的中点,
的中点,
又∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .…4分
.…4分
(2)由![]() 平面
平面![]() ,得
,得![]() ,
, ![]() .
.
以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
设![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() ,
, ![]() 得:
得:
![]() ,令
,令![]() ,得
,得![]()
同理可得平面![]() 的一个法向量为
的一个法向量为![]()
∵平面![]() 平面
平面![]() ,∴
,∴![]()
解得![]() ,得
,得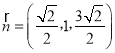 ,又
,又![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
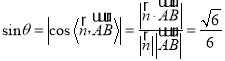 .
.
所以,直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,亚洲热带地区广泛栽培.槟榔是重要的中药材,南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).

(1)你能否估计哪个班的学生平均每周咀嚼槟榔的颗数较多?
(2)在被抽取的10名学生中,从平均每周咀嚼槟榔的颗数不低于20颗的学生中随机抽取3名学生,求抽到![]() 班学生人数
班学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查了解某高等院校毕业生参加工作后,从事对工作与大学所学专业是否专业对口,该校随机调查了80位该校2015年毕业的大学生,得到具体数据如下表:

(1)能否在犯错误的概率不超过![]() 的前提下,认为“毕业生从事的工作与大学所学专业对口与性别有关?”
的前提下,认为“毕业生从事的工作与大学所学专业对口与性别有关?”
参考公式:
附表:

(2)求这80位毕业生从事的工作与大学所学专业对口的概率,并估计该校近3年毕业的2000名大学生总从事的工作与大学所学专业对口的人数;
(3)若从工作与所学专业不对口的15人中选出男生甲、乙,女生对丙、丁,让他们两两进行一次10分钟的职业交流,该校宣传部对每次交流都一一进行视频记录,然后随机选取一次交流视频上传到学校的网站,试求选取的视频恰为异性交流视频的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (
(![]() )的左、右焦点分别是
)的左、右焦点分别是![]() 、
、![]() ,离心率为
,离心率为![]() ,过
,过![]() 且垂直于轴的直线被椭圆C截得的线段长为3.
且垂直于轴的直线被椭圆C截得的线段长为3.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接![]() 、
、![]() ,设
,设![]() 的角平分线PM交C的长轴于点
的角平分线PM交C的长轴于点![]() ,求m的取值范围;
,求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,若
,若![]() ,试证明
,试证明![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则![]() 的最小值为( )
的最小值为( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面推理是类比推理的是( )
A.两条直线平行,则同旁内角互补,若![]() 和
和![]() 是同旁内角,则
是同旁内角,则![]()
B.某校高二有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此推测各班都超过50位团员
C.由平面三角形的面积![]() (其中
(其中![]() 是三角形的周长,
是三角形的周长,![]() 是三角形内切圆的半径),推测空间中三棱锥的体积
是三角形内切圆的半径),推测空间中三棱锥的体积![]() (其中
(其中![]() 是三棱锥的表面积,
是三棱锥的表面积,![]() 是三棱锥内切球的半径)
是三棱锥内切球的半径)
D.一切偶数能被2整除,![]() 是偶数,故
是偶数,故![]() 能被2整数
能被2整数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com