
在平面直角坐标系中,已知点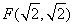 及直线
及直线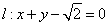 ,曲线
,曲线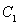 是满足下列两个条件的动点
是满足下列两个条件的动点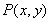 的轨迹:①
的轨迹:①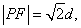 其中
其中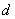 是
是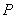 到直线
到直线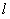 的距离;②
的距离;②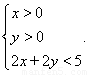
(1) 求曲线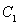 的方程;
的方程;
(2) 若存在直线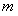 与曲线
与曲线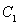 、椭圆
、椭圆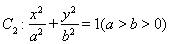 均相切于同一点,求椭圆
均相切于同一点,求椭圆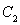 离心率
离心率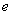 的取值范围.
的取值范围.
(1)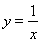
 ;(2)
;(2)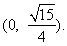
【解析】
试题分析:(1)求出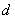 是
是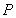 到直线
到直线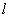 的距离d和
的距离d和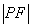 的表达式,由
的表达式,由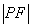 =2d建立等式,整理得
=2d建立等式,整理得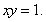 在把
在把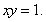 代入
代入 中求出x的取值范围即可.
中求出x的取值范围即可.
(2)由导数的几何意义求出直线m的斜率,求出直线m的参数方程,然后代入曲线C2方程中,消去y得到关于x的一元二次方程,由直线 与椭圆
与椭圆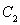 相切,所以△=
相切,所以△=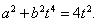
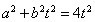 =0,而又
=0,而又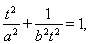 二者联立起来解出a2,b2,由a2>b2,求出参数t的取值范围,在根据椭圆离心率e的定义就可求出其范围.
二者联立起来解出a2,b2,由a2>b2,求出参数t的取值范围,在根据椭圆离心率e的定义就可求出其范围.
试题解析:解:(1)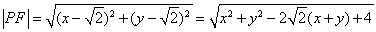 ,
,
 , 2分
, 2分
由①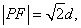 得:
得:
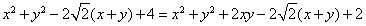 ,
,
即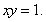 4分
4分
将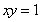 代入②得:
代入②得: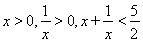 ,
,
解得: 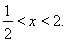
所以曲线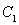 的方程为:
的方程为: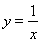
 6分
6分
(2)(解法一)由题意,直线 与曲线
与曲线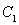 相切,设切点为
相切,设切点为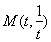 ,
, 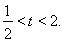
则直线 的方程为
的方程为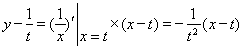 ,
,
即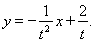 7分
7分
将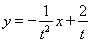 代入椭圆
代入椭圆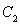 的方程
的方程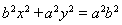 ,并整理得:
,并整理得:
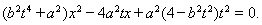
由题意,直线 与椭圆
与椭圆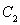 相切于点
相切于点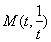 ,则
,则
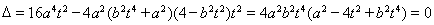 ,
,
即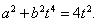 9分
9分
又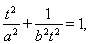 即
即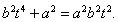 联解得:
联解得: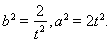 10分
10分
由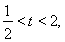 及
及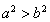 得
得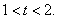
故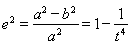 , 12分
, 12分
得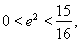 又
又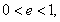 故
故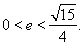
所以椭圆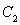 离心率
离心率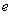 的取值范围是
的取值范围是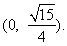 14分
14分
(2)(解法二)设直线 与曲线
与曲线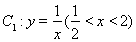 、椭圆
、椭圆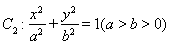 均相切于同一点
均相切于同一点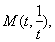 则
则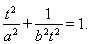 7分
7分
由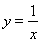 知
知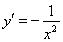 ;
;
由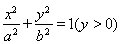 知
知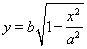 ,
,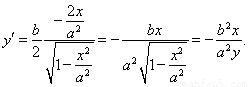
故 9分
9分
联解 ,得
,得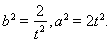 10分
10分
由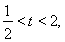 及
及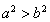 得
得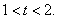
故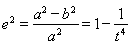 , 12分
, 12分
得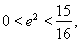 又
又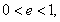 故
故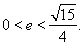
所以椭圆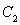 离心率
离心率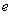 的取值范围是
的取值范围是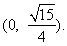 14分
14分
考点:1.点到直线的距离和曲线方程;2.由导数的几何意义;3.直线与曲线的位置关系.


科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com