
分析 (1)由等差数列的通项公式和等比数列的性质,可得首项为1或-9,即可得到所求通项;
(2)求得bn=n•2n,运用错位相减法,结合等比数列的求和公式,计算即可得到.
解答 解:(1)由an+1=an+1,知数列{an}是公差为1的等差数列,
所以a3+1=a1+3,a8=a1+7,
依题意知(a1+3)2=2a1(a1+7),即a12+8a1-9=0,
解得a1=1或a1=-9,
当a1=1时,an=n;
当a1=-9时,an=-10+n;
(2)由(1)知an=n,所以bn=n•2n,
Sn=2+2•22+3•23+…+n•2n①
2Sn=4+2•23+3•24+…+n•2n+1②
①-②得-Sn=2+22+23+…+2n-n•2n+1
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1=(1-n)•2n+1-2,
所以Sn=(n-1)•2n+1+2.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,考查数列的求和方法:错位相减法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ${C}_{4}^{3}$ | B. | A43 | C. | 43 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
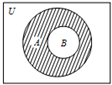 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )| A. | {x|1<x<3} | B. | {x|1<x≤3} | C. | {x|1≤x<3} | D. | {x|1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$-$\frac{3}{2}$i | B. | -$\frac{1}{2}$-$\frac{3}{2}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | -$\frac{1}{2}$+$\frac{3}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
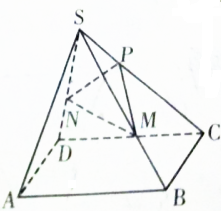 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com