
【题目】设![]() ,函数
,函数![]() ,
,![]() (
(![]() 为自然对数的底数),且函数
为自然对数的底数),且函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 处有公共的切线.
处有公共的切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)证明:当![]() 时,
时,![]() 在区间
在区间![]() 内恒成立.
内恒成立.
【答案】(Ⅰ)![]() (Ⅱ)详见解析(Ⅲ)详见解析
(Ⅱ)详见解析(Ⅲ)详见解析
【解析】
试题分析:(Ⅰ)由导数几何意义得![]() ,分别求导得
,分别求导得![]() (Ⅱ)由于
(Ⅱ)由于![]() ,所以根据导函数是否变号进行讨论:当
,所以根据导函数是否变号进行讨论:当![]() 时,
时,![]() ,
,![]() 在定义域内单调递增,当
在定义域内单调递增,当![]() 时,先增后减再增(Ⅲ)证明不等式恒成立问题,一般转化为对应函数最值问题,即证
时,先增后减再增(Ⅲ)证明不等式恒成立问题,一般转化为对应函数最值问题,即证![]() 的最小值大于零,利用导数研究函数
的最小值大于零,利用导数研究函数![]() 单调性:
单调性:![]() 时,在区间
时,在区间![]() 内单调递减,从而
内单调递减,从而![]()
试题解析:(Ⅰ)![]() ,
,
由![]() ,得
,得![]() .……………………………………2分
.……………………………………2分
(Ⅱ)![]() ,
,
当![]() 时,即
时,即![]() 时,
时,![]() ,从而函数
,从而函数![]() 在定义域内单调递增,
在定义域内单调递增,
当![]() 时,
时,![]() ,此时
,此时
若![]() ,
,![]() ,则函数
,则函数![]() 单调递增;
单调递增;
若![]() ,
,![]() ,则函数
,则函数![]() 单调递减;
单调递减;
若![]() 时,
时,![]() ,则函数
,则函数![]() 单调递增.……………………6分
单调递增.……………………6分
(Ⅲ)令![]() ,则
,则![]() .
.
![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
又当![]() 时,
时,![]() ,从而
,从而![]() 单调递减;
单调递减;
所以![]() .
.
故当![]() 时,
时,![]() 单调递增;
单调递增;
又因为![]() ,故当
,故当![]() 时,
时,![]() ,
,
从而函数![]() 在区间
在区间![]() 单调递减;
单调递减;
又因为![]()
所以![]() 在区间
在区间![]() 恒成立.…………14分
恒成立.…………14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地拟建一座长为640米的大桥![]() ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩![]() 造价总共为100万元,当相邻两个桥墩的距离为
造价总共为100万元,当相邻两个桥墩的距离为![]() 米时(其中
米时(其中![]() ).中间每个桥墩的平均造价为
).中间每个桥墩的平均造价为![]() 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为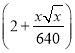 万元.
万元.

(1)试将桥的总造价表示为![]() 的函数
的函数![]() ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩![]() 除外)应建多少个桥墩?
除外)应建多少个桥墩?
查看答案和解析>>
科目:高中数学 来源: 题型:
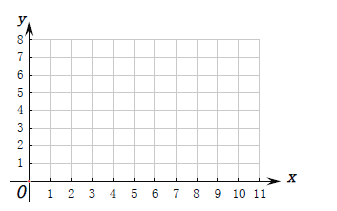
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 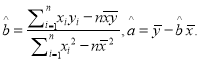
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系?
附: 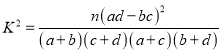
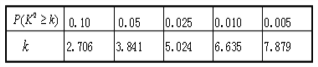
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]()
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 做直线
做直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,若在
两点,若在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的直角三角形,求直线
为直角顶点的直角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地自来水苯超标,当地自来水公司对水质检测后,决定在水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中 ,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为![]() ,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com