
【题目】已知![]() .
.
(1)当![]() 为常数,且
为常数,且![]() 在区间
在区间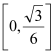 变化时,求
变化时,求![]() 的最小值
的最小值![]() ;
;
(2)证明:对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() .
.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
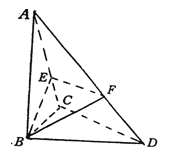
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:
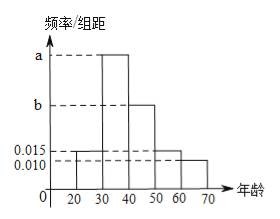
【题目】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如右图.
位上网购物者的年龄情况如右图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() (
(![]() 为自然对数的底数),且函数
为自然对数的底数),且函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 处有公共的切线.
处有公共的切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)证明:当![]() 时,
时,![]() 在区间
在区间![]() 内恒成立.
内恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 和抛物线
和抛物线![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 恰好通过椭圆
恰好通过椭圆![]() 的右焦点.
的右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过椭圆![]() 右焦点的直线
右焦点的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在椭圆上,且
在椭圆上,且![]() ,
,
其中![]() 为坐标原点,求直线
为坐标原点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com