
【题目】已知函数![]() ,
, ![]()
(1)若![]() 的一个极值点到直线
的一个极值点到直线![]() 的距离为1,求
的距离为1,求![]() 的值;
的值;
(2)求方程![]() 的根的个数
的根的个数
【答案】(1)a=-2或a=-8.(2)见解析
【解析】试题分析:(1)先求出函数![]() 的导函数
的导函数![]() ,令
,令![]() ,可得函数只有一个极值点,根据点到直线的距离公式可得结果;(2)
,可得函数只有一个极值点,根据点到直线的距离公式可得结果;(2)![]() 根的个数等价于
根的个数等价于![]() 的零点个数,利用导数研究函数的单调性,可得结果.
的零点个数,利用导数研究函数的单调性,可得结果.
试题解析:(1)由f′(x)=![]() =0,得x=0,
=0,得x=0,
故f(x)仅有一个极小值点M(0,0),
根据题意得:
d=![]() =1.
=1.
∴a=-2或a=-8.
(2)令h(x)=f(x)-g(x)=ln(x2+1)-![]() -a,
-a,
h′(x)=![]() +
+![]() =2x
=2x![]() .
.
当x∈(0,1)∪(1,+∞)时,h′(x)≥0,
当x∈(-∞,-1)∪(-1,0)时,h′(x)<0.
因此,h(x)在(-∞,-1),(-1,0)上时,h(x)单调递减,
在(0,1),(1,+∞)上时,h(x)单调递增.
又h(x)为偶函数,当x∈(-1,1)时,h(x)的极小值为h(0)=1-a.
当x→-1-时,h(x)→-∞,当x→-1+时,h(x)→+∞,
当x→-∞时,h(x)→+∞,当x→+∞时,h(x)→+∞.
由根的存在性定理知,方程在(-∞,-1)和(1,+∞)一定有根
故f(x)=g(x)的根的情况为:
当1-a>0时,即a<1时,原方程有2个根;
当1-a=0时,即a=1时,原方程有3个根.
当1-a<0时,即a>1时,原方程有4个根.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试求
,试求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

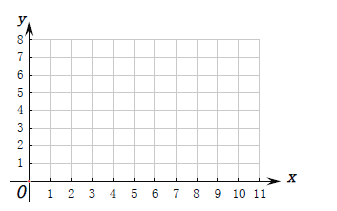
(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 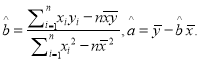
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com