
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 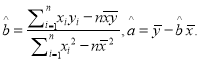
![]()
科目:高中数学 来源: 题型:
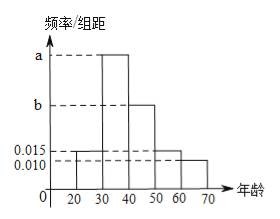
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如右图.
位上网购物者的年龄情况如右图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() (
(![]() 为自然对数的底数),且函数
为自然对数的底数),且函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 处有公共的切线.
处有公共的切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)证明:当![]() 时,
时,![]() 在区间
在区间![]() 内恒成立.
内恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com