
【题目】已知函数![]() ,其中
,其中![]() 、
、![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() 是函数
是函数![]() 的导函数,求函数
的导函数,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:讨论![]() 在
在![]() 上的最小值必然要讨论
上的最小值必然要讨论![]() 在
在![]() 上的正负情况,当
上的正负情况,当![]() 在
在![]() 上单调递增时,
上单调递增时, ![]() 恒成立,必有
恒成立,必有![]() 即
即![]() 当
当![]() 在
在![]() 上单调递减时,
上单调递减时, ![]() 恒成立,必有
恒成立,必有![]() 即
即![]() 当
当![]() 在
在![]() 上不单调时,必有
上不单调时,必有![]() 分三种情况讨论.
分三种情况讨论.
试题解析:
由![]() ,有
,有
由![]() ,
,
∴![]() .
.
当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
因此![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
因此![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,令
时,令![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
于是![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
综上所述,当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最小值是
上的最小值是![]() .
.
点睛:本题考查含参量函数的最值问题,属于难题. ![]() 中含有两个参数,且
中含有两个参数,且![]() 为非基本初等函数,所以只能研究
为非基本初等函数,所以只能研究![]() 的正负来确定
的正负来确定![]() 在
在![]() 上的单调情况,从而求出
上的单调情况,从而求出![]() 在
在![]() 上的最值,还可以研究
上的最值,还可以研究![]() 的图像来确定
的图像来确定![]() 的正负.
的正负.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(Ⅰ)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)若函数![]() 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为![]() ,证明
,证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地拟建一座长为640米的大桥![]() ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩![]() 造价总共为100万元,当相邻两个桥墩的距离为
造价总共为100万元,当相邻两个桥墩的距离为![]() 米时(其中
米时(其中![]() ).中间每个桥墩的平均造价为
).中间每个桥墩的平均造价为![]() 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为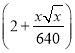 万元.
万元.

(1)试将桥的总造价表示为![]() 的函数
的函数![]() ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩![]() 除外)应建多少个桥墩?
除外)应建多少个桥墩?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

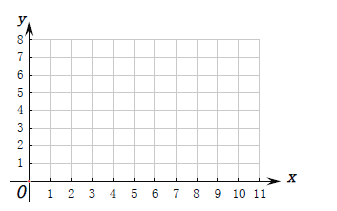
(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 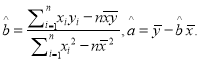
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com