
【题目】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)先求函数的定义域,再求函数的导数,![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性和单调区间;(Ⅱ)首先求
两种情况讨论函数的单调性和单调区间;(Ⅱ)首先求![]() ,因为
,因为![]() ,所以设
,所以设![]() ,求函数的导数
,求函数的导数![]() ,因为不能判断导函数的正负或是单调性,所以再求
,因为不能判断导函数的正负或是单调性,所以再求![]() ,这样可分
,这样可分![]() ,
,![]() 和
和![]() 的情况讨论
的情况讨论![]() 的正负,从而得到
的正负,从而得到![]() 的单调性以及最小值,进一步得到
的单调性以及最小值,进一步得到![]() 的单调性和最值,即证明
的单调性和最值,即证明![]() ,得到
,得到![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
① ![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
② 若![]() ,则由
,则由![]() ,得
,得![]() ,
,
当![]()
![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
综上:当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ) ![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
①若![]() ,
,![]() ,
,![]() 在
在![]() 递增,
递增,![]() ,
,
![]() 在
在![]() 上递增,
上递增,![]() ,
,
从而![]() ,不符合题意,
,不符合题意,
②若![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
从而![]() ,
,
![]() 在
在![]() 上递增,
上递增,![]() ,
,
从而![]() ,不符合题意,
,不符合题意,
③若![]() ,
,![]() 在
在![]() 恒成立,
恒成立,
![]() 在在
在在![]() 递减,
递减,![]() ,
,
从而![]() 在
在![]() 递减,
递减,
![]()
所以![]() ,
,
综上所述:![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
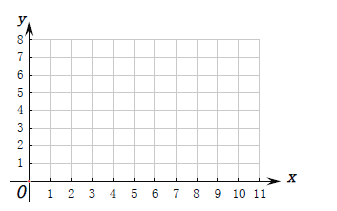
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 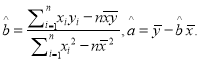
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地自来水苯超标,当地自来水公司对水质检测后,决定在水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中 ,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为![]() ,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试求
,试求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象上有一点列
的图象上有一点列![]() ,点
,点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() (
(![]() 且
且![]() ),
), ![]() .
.
(1)求证: ![]() 是等比数列,并求出数列
是等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)对任意的正整数![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设四边形![]() 的面积是
的面积是![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com