
【题目】某高新技术公司要生产一批新研发的![]() 款手机和
款手机和![]() 款手机,生产一台
款手机,生产一台![]() 款手机需要甲材料
款手机需要甲材料![]() ,乙材料
,乙材料![]() ,并且需要花费1天时间,生产一台
,并且需要花费1天时间,生产一台![]() 款手机需要甲材料
款手机需要甲材料![]() ,乙材料
,乙材料![]() ,也需要1天时间,已知生产一台
,也需要1天时间,已知生产一台![]() 款手机利润是1000元,生产一台
款手机利润是1000元,生产一台![]() 款手机的利润是2000元,公司目前有甲、乙材料各,则在
款手机的利润是2000元,公司目前有甲、乙材料各,则在![]() 不超过120天的情况下,公司生产两款手机的最大利润是__________元.
不超过120天的情况下,公司生产两款手机的最大利润是__________元.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.
(Ⅰ)求圆的方程;
(Ⅱ)设直线ax﹣y+5=0(a>0)与圆相交于A,B两点,求实数a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数a,使得弦AB的垂直平分线l过点P(﹣2,4),若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产![]() 、
、![]() 两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
产品 | 8 | 12 | 40 | 32 | 8 |
产品 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)请估计![]() 产品的一等奖;
产品的一等奖;
(Ⅱ)已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
(i)分别估计生产一件![]() 产品,一件
产品,一件![]() 产品的利润大于0的概率;
产品的利润大于0的概率;
(ii)请问生产![]() 产品,
产品, ![]() 产品各100件,哪一种产品的平均利润比较高.
产品各100件,哪一种产品的平均利润比较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= ![]() .
.
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A﹣EF﹣C的大小为60°?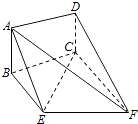
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com