
分析 用$\overrightarrow{AD},\overrightarrow{BE}$表示出$\overrightarrow{AB},\overrightarrow{AC}$,代入$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{2}{3}$得出$\overrightarrow{AD}$•$\overrightarrow{BE}$,即可求得夹角.
解答 解: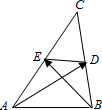 ∵AD、BE分别是△ABC的中线,
∵AD、BE分别是△ABC的中线,
∴$\left\{\begin{array}{l}{\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}}\\{\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BE}}\end{array}\right.$,又$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,
∴$\left\{\begin{array}{l}{\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}}\\{\overrightarrow{AC}-2\overrightarrow{AB}=2\overrightarrow{BE}}\end{array}\right.$,
∴$\overrightarrow{AB}$=$\frac{2}{3}\overrightarrow{AD}-\frac{2}{3}\overrightarrow{BE}$,$\overrightarrow{AC}$=$\frac{4}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BE}$.
∴且$\overrightarrow{AB}$•$\overrightarrow{AC}$=($\frac{2}{3}\overrightarrow{AD}-\frac{2}{3}\overrightarrow{BE}$)•($\frac{4}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BE}$)=$\frac{8}{9}{\overrightarrow{AD}}^{2}$-$\frac{4}{9}{\overrightarrow{BE}}^{2}$-$\frac{4}{9}$$\overrightarrow{AD}•\overrightarrow{BE}$=$\frac{2}{3}$,
∵${\overrightarrow{AD}}^{2}={\overrightarrow{BE}}^{2}=1$,
∴$\overrightarrow{AD}•\overrightarrow{BE}=-\frac{1}{2}$.
∴cos<$\overrightarrow{AD},\overrightarrow{BE}$>=$\frac{\overrightarrow{AD}•\overrightarrow{BE}}{|\overrightarrow{AD}||\overrightarrow{BE}|}$=-$\frac{1}{2}$.
∴$\overrightarrow{AD}$与$\overrightarrow{BE}$的夹角为$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查了平面向量线性运算的几何意义,平面向量的数量积运算,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | 1 | C. | -1 | D. | ±$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
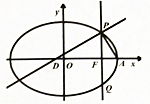 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com