
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,判断
时,判断![]() 是否是函数
是否是函数![]() 的极值点,并说明理由;
的极值点,并说明理由;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
【答案】(1)![]() 是函数
是函数![]() 的极大值点,理由详见解析;(2)1.
的极大值点,理由详见解析;(2)1.
【解析】
(1)将![]() 直接代入,对
直接代入,对![]() 求导得
求导得![]() ,由于函数单调性不好判断,故而构造函数,继续求导,判断导函数
,由于函数单调性不好判断,故而构造函数,继续求导,判断导函数![]() 在
在![]() 左右两边的正负情况,最后得出,
左右两边的正负情况,最后得出,![]() 是函数
是函数![]() 的极大值点;
的极大值点;
(2)利用题目已有条件得![]() ,再证明
,再证明![]() 时,不等式
时,不等式![]() 恒成立,即证
恒成立,即证![]() ,从而可知整数
,从而可知整数![]() 的最小值为1.
的最小值为1.
解:(1)当![]() 时,
时,![]() .
.
令![]() ,则
,则![]()
当![]() 时,
时,![]() .
.
即![]() 在
在![]() 内为减函数,且
内为减函数,且![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 内是增函数,在
内是增函数,在![]() 内是减函数.
内是减函数.
综上,![]() 是函数
是函数![]() 的极大值点.
的极大值点.
(2)由题意,得![]() ,即
,即![]() .
.
现证明当![]() 时,不等式
时,不等式![]() 成立,即
成立,即![]() .
.
即证![]()
令![]()
则![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
![]() 的最大值为
的最大值为![]() .
.
∴当![]() 时,
时,![]() .
.
即当![]() 时,不等式
时,不等式![]() 成立.
成立.
综上,整数![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线l的参数方程为![]() (t为参数,0<α<π),以坐标原点为极点,x轴正半轴为极轴建立及坐标系,曲线C:ρsin2θ=4cosθ.
(t为参数,0<α<π),以坐标原点为极点,x轴正半轴为极轴建立及坐标系,曲线C:ρsin2θ=4cosθ.
(1)求l和C的直角坐标方程;
(2)若l与C相交于A,B两点,且|AB|![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角α﹣l﹣β为60°,在其内部取点A,在半平面α,β内分别取点B,C.若点A到棱l的距离为1,则△ABC的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.

(1)若![]() 米,求
米,求![]() 的长;
的长;
(2)设![]() , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
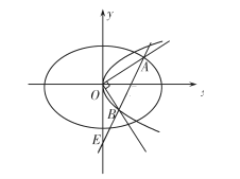
【题目】已知抛物线![]() 与
与
椭圆![]() 的一个交点为
的一个交点为![]() ,点
,点![]()
是![]() 的焦点,且
的焦点,且![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
(2)设![]() 为坐标原点,在第一象限内,椭圆
为坐标原点,在第一象限内,椭圆![]() 上是否存在点
上是否存在点![]() ,使过
,使过![]() 作
作![]() 的垂线交抛物线
的垂线交抛物线![]() 于
于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ?若存在,求出点
?若存在,求出点![]() 的坐标和
的坐标和![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
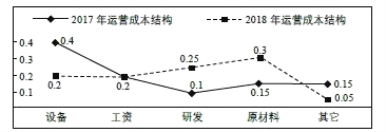
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面多边形![]() 中,四边形
中,四边形![]() 是边长为2的正方形,四边形
是边长为2的正方形,四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,
的中点,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
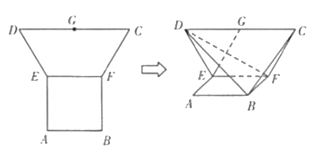
(1)求证:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com