
【题目】在直角坐标系xOy中,曲线l的参数方程为![]() (t为参数,0<α<π),以坐标原点为极点,x轴正半轴为极轴建立及坐标系,曲线C:ρsin2θ=4cosθ.
(t为参数,0<α<π),以坐标原点为极点,x轴正半轴为极轴建立及坐标系,曲线C:ρsin2θ=4cosθ.
(1)求l和C的直角坐标方程;
(2)若l与C相交于A,B两点,且|AB|![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() x=1或y=tanα(x﹣1),曲线C:y2=4x.(2)
x=1或y=tanα(x﹣1),曲线C:y2=4x.(2)![]() 或
或![]()
【解析】
![]() 对于曲线
对于曲线![]() :分
:分![]() 和
和![]() 两种情况分别消去参数
两种情况分别消去参数![]() 求解即可;对于曲线C:方程两边同时乘以
求解即可;对于曲线C:方程两边同时乘以![]() ,利用转换公式
,利用转换公式![]() 即可求解.
即可求解.
![]() 把曲线l的参数方程
把曲线l的参数方程![]() ,代入y2=4x,得到关于
,代入y2=4x,得到关于![]() 的一元二次方程,利用韦达定理求出
的一元二次方程,利用韦达定理求出![]() ,根据参数
,根据参数![]() 的几何意义知,
的几何意义知,![]() ,代入即可求解.
,代入即可求解.
(1)曲线l的参数方程为![]() (t为参数,0<α<π),
(t为参数,0<α<π),
当![]() 时,直线的直角坐标方程为x=1.
时,直线的直角坐标方程为x=1.
当![]() 时,直线的直角坐标方程为y=tanα(x﹣1).
时,直线的直角坐标方程为y=tanα(x﹣1).
因为曲线C:ρsin2θ=4cosθ,
方程两边同时乘以![]() 可得,曲线C:
可得,曲线C:![]() ,
,
因为![]() ,
,
所以曲线C的直角坐标方程为y2=4x.
(2)把曲线l的参数方程![]() ,代入y2=4x,
,代入y2=4x,
得到sin2αt2﹣4cosαt﹣4=0,
所以![]() ,
,![]() ,
,
所以![]() ,
,
即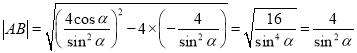 ,
,
所以![]() ,整理得
,整理得![]() ,
,
所以![]() (0<α<π),
(0<α<π),
所以![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
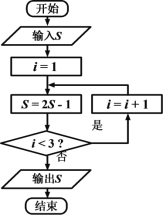
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区,在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择5个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以该小区的个体经营户为样本,频率作为概率,从全国个体经营户中随机选择3家作为普查对象,入户登记顺利的对象数记为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了了解市民搭乘公共交通工具的出行情况,收集并整理了2017年全年每月公交和地铁载客量的数据,绘制了下面的折线图:
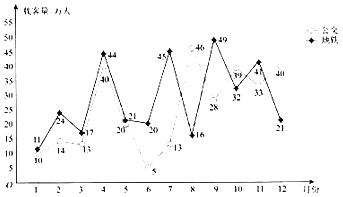
根据该折线图,下列结论错误的是( )
A.全年各月公交载客量的极差为41B.全年各月地铁载客量的中位数为22.5
C.7月份公交与地铁的载客量相差最多D.全年地铁载客量要小于公交载客量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
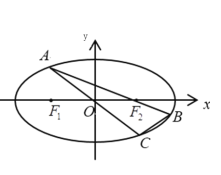
(1)求椭圆的标准方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com