
【题目】设函数\![]() .
.
(1)若![]() 且
且![]() 在
在![]() 处的切线垂直于y轴,求a的值;
处的切线垂直于y轴,求a的值;
(2)若对于任意![]() ,都有
,都有![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)1;(2)![]() .
.
【解析】
(1)先求得![]() 的导函数,根据
的导函数,根据![]() 在
在![]() 处的切线垂直于y轴可知在
处的切线垂直于y轴可知在![]() 处的导数等于0,代入即可求得
处的导数等于0,代入即可求得![]() 的值.
的值.
(2)根据任意![]() ,都有
,都有![]() 恒成立,则
恒成立,则![]() 成立,代入可得
成立,代入可得![]() .结合函数单调性,使得
.结合函数单调性,使得![]() 在
在![]() 上满足单调递增且
上满足单调递增且![]() ,即可得
,即可得![]() 的取值范围.再利用构造函数法,证明
的取值范围.再利用构造函数法,证明![]() 在
在![]() 时满足单调递增即可.
时满足单调递增即可.
(1)![]() ,则
,则![]() ,∴
,∴![]() ,
,
∵![]() 且
且![]() 在
在![]() 处的切线垂直于y轴,
处的切线垂直于y轴,
∴![]() ,∴
,∴![]() ,又
,又![]()
∴![]()
(2)对于任意![]() ,都有
,都有![]() 恒成立,则
恒成立,则![]() ,所以
,所以![]() ,
,
![]() ,
,![]() ,
,![]() ,得
,得![]() ,所以
,所以![]() ,即
,即![]() ,
,
下面证明![]() 成立,
成立,
∴![]() ,令
,令![]() ,
,![]() ,
,
∴令![]() ,
,![]() ,∴
,∴![]() ,
,
∴函数![]() 在
在![]() 上单调递增,由
上单调递增,由![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() ,∴函数
,∴函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 成立,
成立,
所以![]() 对于任意
对于任意![]() ,都有
,都有![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ,而
,而![]() 在
在![]() 上单调递增,
上单调递增,
∴存在唯一的![]() ,使得
,使得![]() ,即
,即![]() ,
,![]() ,
,
且![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,
单调递增,
![]() ,而
,而![]() ,
,
令![]() ,
,
∴![]() ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
![]() 或
或![]() 时,
时,![]() 单调递减,
单调递减,![]() 时,
时,![]() 单调递增,
单调递增,
∴![]() 是
是![]() 的极小值,而
的极小值,而![]() ,∴当
,∴当![]() 时,
时,![]() 有小于0的函数值,也即是
有小于0的函数值,也即是![]() 有小于0的函数值,这与对于任意
有小于0的函数值,这与对于任意![]() ,都有
,都有![]() 恒成立,相矛盾,∴当
恒成立,相矛盾,∴当![]() 时,不满足题意,
时,不满足题意,
综上可得,a的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某飞机失联,经卫星侦查,其最后出现在小岛![]() 附近,现派出四艘搜救船
附近,现派出四艘搜救船![]() ,为方便联络,船
,为方便联络,船![]() 始终在以小岛
始终在以小岛![]() 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船![]() 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛![]() 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() ,
,![]() 船到小岛
船到小岛![]() 的距离为
的距离为![]() .
.
(1)请分别求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并分别写出定义域;
,并分别写出定义域;
(2)当![]() 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即![]() 最大)?
最大)?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中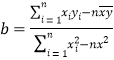 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
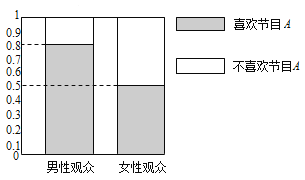
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
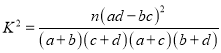 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 为
为![]() 上的动点,
上的动点,![]() 点满足
点满足![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以为![]() 极点,
极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在平面四边形ABCD中,AC是BD的垂直平分线,垂足为E,AB中点为F,![]() ,
,![]() ,
,![]() ,沿BD将
,沿BD将![]() 折起,使C至
折起,使C至![]() 位置,如图(2).
位置,如图(2).
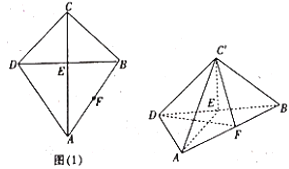
(1)求证:![]() ;
;
(2)当平面![]() 平面ABD时,求直线
平面ABD时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com