
【题目】已知圆M的圆心M在x轴上,半径为![]() ,直线
,直线![]() 被圆M截得的弦长为
被圆M截得的弦长为![]() ,且圆心M在直线l的上方.
,且圆心M在直线l的上方.
(1)求圆![]() 的方程;
的方程;
(2)设![]() ,
,![]()
![]() ,若圆M是
,若圆M是![]() 的内切圆,求AC,BC边所在直线的斜率(用t表示);
的内切圆,求AC,BC边所在直线的斜率(用t表示);
(3)在(2)的条件下求![]() 的面积S的最大值及对应的t值.
的面积S的最大值及对应的t值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】滕州市教育局为了解学生网络教学期间的学习情况,从初中及高中共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
年级 | 人数 |
初一 | 4 |
初二 | 4 |
初三 | 6 |
高一 | 12 |
高二 | 6 |
高三 | 18 |
合计 | 50 |

(1)抽查的50人中,每天平均学习时间为6~8小时的人数有多少?
(2)经调查,每天平均学习时间不少于6小时的学生均来自高中.现采用分层抽样的方法,从学习时间不少于6小时的学生中随机抽取6名学生进行问卷调查,求这三个年级各抽取了多少名学生;
(3)在(2)抽取的6名学生中随机选取2人进行访谈,求这2名学生来自不同年级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的侧棱与底面垂直,
的侧棱与底面垂直,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.

(Ⅰ)证明:无论![]() 取何值,总有
取何值,总有![]() ;
;
(Ⅱ)当![]() 取何值时,直线
取何值时,直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 最大?并求该角取最大值时的正切值.
最大?并求该角取最大值时的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
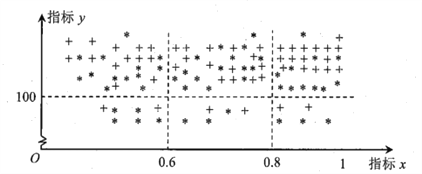
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,短轴长为![]() ,离心率为
,离心率为![]() .
.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 若过点
若过点![]() 的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
的直线与椭圆C交于A,B两点,且P点平分线段AB,求直线AB的方程;
![]() Ⅲ
Ⅲ![]() 一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,
一条动直线l与椭圆C交于不同两点M,N,O为坐标原点,![]() 的面积为
的面积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个计算装置有两个数据输入端口I,II与一个运算结果输出端口III,当I,II分别输入正整数![]() 时,输出结果记为
时,输出结果记为![]() 且计算装置运算原理如下:
且计算装置运算原理如下:
①若I,II分别输入![]() 则
则![]()
②若I输入固定的正整数![]() II输入的正整数增大
II输入的正整数增大![]() 则输出的结果比原来增大
则输出的结果比原来增大![]()
③若II输入![]() I输入正整数增大
I输入正整数增大![]() 则输出结果为原来的
则输出结果为原来的![]() 倍.则(1)
倍.则(1)![]() =
= ![]() 为正整数);(2)(1)f(m,1)=__,(2)若由f(m,1)得出f(m,n),则满足f(m,n)=30的平面上的点(m,n)的个数是__.
为正整数);(2)(1)f(m,1)=__,(2)若由f(m,1)得出f(m,n),则满足f(m,n)=30的平面上的点(m,n)的个数是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某城市居民家庭年收入![]() (万元)和年“享受资料消费”
(万元)和年“享受资料消费”![]() (万元)进行统计分析,得数据如表所示.
(万元)进行统计分析,得数据如表所示.
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |
(1)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)若某家庭年收入为18万元,预测该家庭年“享受资料消费”为多少?
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如下,已知分数在100~110的学生数有21人。

(Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩。
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某建筑公司打算在一处工地修建一座简易储物间.该储物间室内地面呈矩形形状,面积为![]() ,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为
,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/米,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为![]() 米.
米.

(1)用![]() 表示修建储物间的总造价
表示修建储物间的总造价![]() (单位:元);
(单位:元);
(2)如何设计该储物间,可使总造价最低?最低总造价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com