
(本小题12分)如图,设抛物线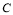 :
: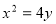 的焦点为F,
的焦点为F,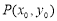 为抛物线上的任一点(其
为抛物线上的任一点(其
中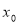 ≠0),过P点的切线交
≠0),过P点的切线交 轴于
轴于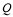 点.
点.
(1)若 ,求证
,求证 ;
;
(2)已知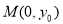 ,过M点且斜率为
,过M点且斜率为 的直线与抛物线
的直线与抛物线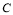 交于A、B两点,若
交于A、B两点,若 ,求
,求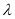 的值.
的值.
(1)证明见解析,(2)
【解析】
试题分析:要证明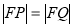 ,由
,由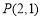 在抛物线上,利用焦半径公式
在抛物线上,利用焦半径公式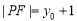 求出,过点
求出,过点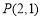 斜率为
斜率为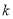 的直线可设为点斜式,与抛物线联立,由于相切,则可借助判别式为0,求出
的直线可设为点斜式,与抛物线联立,由于相切,则可借助判别式为0,求出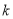 ,得出切线方程,再找出切线与
,得出切线方程,再找出切线与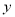 轴的交点
轴的交点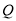 ,进而求出
,进而求出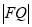 ,得出所证的结论.(2)利用点斜式写出直线方程
,得出所证的结论.(2)利用点斜式写出直线方程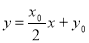 ,与抛物线方程联立消去
,与抛物线方程联立消去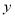 后,得到关于
后,得到关于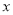 的一元二次方程,于是得出
的一元二次方程,于是得出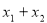 和
和 ,通过
,通过 找出
找出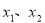 的关系,代入
的关系,代入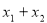 和
和 即可就出
即可就出 .
.
试题解析:(Ⅰ)证明:由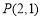 在抛物线上,利用抛物线定义知
在抛物线上,利用抛物线定义知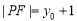
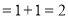
设过P点的切线方程为 ,由
,由
 ,
,
令 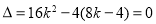 得
得 ,切线方程
,切线方程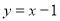 ,
,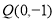 ,∴
,∴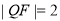 ,即 |PF|=|QF|;
,即 |PF|=|QF|;
(Ⅱ)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0) ∴AB方程为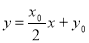 ,由
,由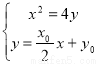 得
得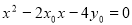 ,∴
,∴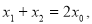
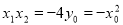 ……① ,由
……① ,由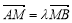 得:
得:
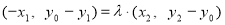 ,∴
,∴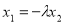 ……② , 由①②知
……② , 由①②知 ,
,
得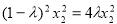 ,由
,由 可得
可得 ,∴
,∴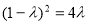 ,又
,又 ,解得:
,解得: .
.
考点:1.抛物线定义;2.焦半径公式;3.直线方程的点斜式;3.设而不求思想;4.一元二次方程的根与系数关系;5.代入减元思想;


科目:高中数学 来源:2014-2015学年甘肃省高一上学期期末考试数学试卷(解析版) 题型:选择题
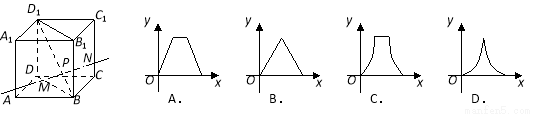
如图,动点 在正方体
在正方体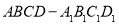 的对角线
的对角线 上,过点
上,过点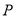 作垂直于平面
作垂直于平面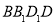 的直线,与正方体表面相交于
的直线,与正方体表面相交于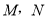 .设
.设 ,
, ,则函数
,则函数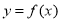 的图象大致是 ( )
的图象大致是 ( )
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期期末考试数学试卷(解析版) 题型:选择题
如果命题p?q为真命题,p?q为假命题,那么( )
A.命题p、q都是真命题
B.命题p、q都是假命题
C.命题p、q只有一个真命题
D.命题p、q至少有一个是真命题
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
将一个白色、一个黄色乒乓球随意地装入甲、乙、丙三个口袋中,则甲口袋中恰好装有乒乓球的概率为( )
A.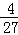 B.
B.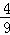 C.
C.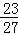 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习理科数学试卷(解析版) 题型:选择题
已知等比数列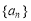 前
前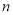 项和为
项和为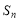 ,则下列一定成立的是
,则下列一定成立的是
A.若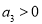 ,则
,则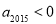 B.若
B.若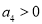 ,则
,则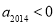
C.若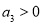 ,则
,则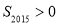 D.若
D.若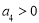 ,则
,则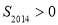
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com