
函数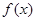 的定义域为
的定义域为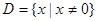 ,且满足对于任意
,且满足对于任意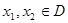 ,有
,有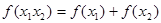 .
.
⑴求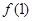 的值;
的值;
⑵判断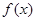 的奇偶性并证明;
的奇偶性并证明;
⑶如果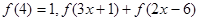 ≤
≤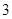 ,且
,且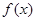 在
在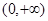 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某单位决定投资3 200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米造价45元,屋顶每平方米造价20元,试计算:
(1)仓库面积S的最大允许值是多少?
(2)为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,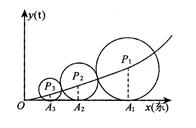
其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点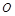 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线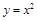 的一段,在小道上依次以点
的一段,在小道上依次以点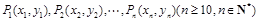 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道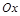 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若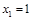 (单位:百米)且
(单位:百米)且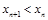 .
.
(1)记以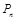 为圆心的圆与主干道
为圆心的圆与主干道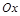 切于
切于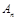 点,证明:数列
点,证明:数列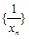 是等差数列,并求
是等差数列,并求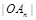 关于
关于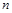 的表达式;
的表达式;
(2)记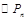 的面积为
的面积为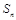 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为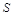 的圆型小道的施工工时为
的圆型小道的施工工时为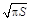 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前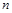 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
(I)求f(x)的解析式;
(II)已知k的取值范围为[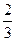 ,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区预计明年从年初开始的前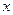 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量 (万件)与月份
(万件)与月份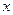 的近似关系为
的近似关系为 .
.
(1)写出明年第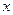 个月的需求量
个月的需求量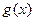 (万件)与月份
(万件)与月份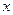 的函数关系式,并求出哪个月份的需求量超过1.4万件;
的函数关系式,并求出哪个月份的需求量超过1.4万件;
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在边长为60cm的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?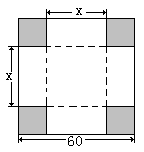
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com