
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
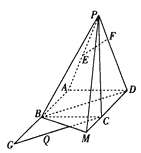
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,二面角
上运动时,二面角![]() 能否等于
能否等于![]() ?请说明理由.
?请说明理由.
【答案】(1)见解析;(2)不能,理由见解析
【解析】
(1)通过证明四边形![]() 是平行四边形,得到
是平行四边形,得到![]() 即可得证;
即可得证;
(2)建立空间直角坐标系,利用空间向量法求出二面角.
解:(1)证明:记![]() 的中点为
的中点为![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() ,且
,且![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,易求
,易求![]() ,
,![]() .
.
又![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
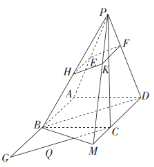
(2)解:因为![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() 是正方形,所以
是正方形,所以![]() .
.
因为![]() 与
与![]() 显然是相交直线,所以
显然是相交直线,所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
记![]() 的中点为
的中点为![]() ,则
,则![]() 平面
平面![]() ,且
,且![]() .
.
以点![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则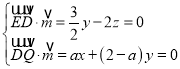 ,
,
令![]() ,得
,得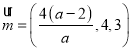 .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的大小是
的大小是![]() ,则
,则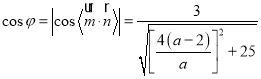 .
.
因为![]() ,所以
,所以![]() ,则
,则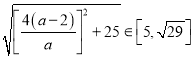 ,
,
所以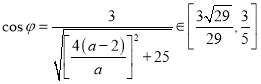 ,
,
因为![]() ,所以
,所以![]() ,即二面角
,即二面角![]() 不可能为
不可能为![]() .
.



 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在四面体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.则下述结论:
的中点.则下述结论:
①四面体![]() 的体积为
的体积为![]() ;
;
②异面直线![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
③四面体![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若用一个与直线![]() 垂直,且与四面体的每个面都相交的平面
垂直,且与四面体的每个面都相交的平面![]() 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为![]() .
.
其中正确的有_____.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日,济南轨道交通![]() 号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
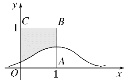
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
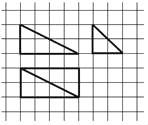
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com