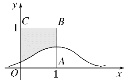
[题目]设X-N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)＝0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )(附:随机变量ξ服从正态分布N(μ.σ2).则P(μ-σ＜ξ＜μ+σ)＝68.26%.P(μ-2σ＜ξ＜μ+2σ)＝95.44%)A. 6038 B. 6587 C. 7028 D. 75 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设X～N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)＝0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为(　　)

(附：随机变量ξ服从正态分布N(μ，σ2)，则P(μ－σ＜ξ＜μ＋σ)＝68.26%，P(μ－2σ＜ξ＜μ＋2σ)＝95.44%)

A. 6038 B. 6587 C. 7028 D. 7539

【答案】B

【解析】分析：求出，即可得出结论.

详解：由题意得，P(X≤－1)＝P(X≥3)＝0.0228，

∴P(－1＜X＜3)＝1－0.022 8×2＝0.954 4，∴1－2σ＝－1，σ＝1，

∴P(0≤X≤1)＝P(0≤X≤2)＝0.341 3，

故估计的个数为10000×(1－0.3413)＝6587，

故选：B.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】2015年推出一种新型家用轿车，购买时费用为16.9万元，每年应交付保险费、养路费及汽油费共1.2万元，汽车的维修费为：第一年无维修费用，第二年为0.2万元，从第三年起，每年的维修费均比上一年增加0.2万元.

（I）设该辆轿车使用n年的总费用（包括购买费用、保险费、养路费、汽油费及维修费）为f(n)，求f(n)的表达式；

（II）这种汽车使用多少报废最合算（即该车使用多少年，年平均费用最少）？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB，则CD与平面BDC1所成角的正弦值等于（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将函数f（x）=sinx的图象向右平移个单位后得到函数y=g（x）的图象，则函数y=f（x）+g（x）的最大值为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某大学生参加社会实践活动，对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查，销售单价x和销售量y之间的一组数据如下表所示：

月份	1	2	3	4	5	6
销售单价（元）	9	9.5	10	10.5	11	8
销售量（件）	11	10	8	6	5	14.2

（1）根据1至5月份的数据，求出y关于x的回归直线方程；

（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，则认为所得到的回归直线方程是理想的，试问（1）中所得到的回归直线方程是否理想？

（3）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？（注：利润=销售收入-成本）．

参考公式：回归直线方程,其中，

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，然后在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒（如图）．设小正方形边长为x厘米，矩形纸板的两边AB，BC的长分别为a厘米和b厘米，其中a≥b．
（1）当a=90时，求纸盒侧面积的最大值；
（2）试确定a，b，x的值，使得纸盒的体积最大，并求出最大值．