
 ,试验不成功的概率都是
,试验不成功的概率都是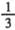 甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.
甲随机地从两套方案中选取一套进行这项试验,共试验了 3次,每次实验相互独立,且要从两套方案中等可能地选择一套.科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个小球,
个小球, 个白球,记为
个白球,记为 ,
, 个红球, 记为
个红球, 记为 ,
, 个黑球, 记为
个黑球, 记为 ,除了颜色和编号外,球没有任何区别.
,除了颜色和编号外,球没有任何区别. 分,取红球得
分,取红球得 分,取黑球得
分,取黑球得 分,求两次取球得分之和为
分,求两次取球得分之和为 分的概率
分的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
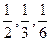 (总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(总项目数足够多),现有3名工人独立地从中任选一个项目参与建设 类别相同的概率;
类别相同的概率;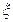 为3人中选择的项目属于B类工程或C类工程的人数,求
为3人中选择的项目属于B类工程或C类工程的人数,求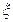 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
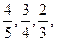 且每个问题回答正确与否相互独立。
且每个问题回答正确与否相互独立。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com