
已知数列{an}和{bn}满足:a1=![]() ,an+1=
,an+1=![]() an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中![]() 为实数,n为正整数.
为实数,n为正整数.
(1)证明:对任意实数![]() ,数列{an}不是等比数列;
,数列{an}不是等比数列;
(2)证明:当![]() ≠-18时,数列{bn}是等比数列;
≠-18时,数列{bn}是等比数列;
(3)设Sn为数列{bn}的前n项和.是否存在实数![]() ,使得对任意正整数n,都有Sn>-12?若存在,求
,使得对任意正整数n,都有Sn>-12?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(1)证明见解析(2)证明见解析(3)存在实数![]() ,使得对任意正整数n都有Sn>-12,
,使得对任意正整数n都有Sn>-12,![]() 的取值范围为(-∞,-6)
的取值范围为(-∞,-6)
(1)证明 假设存在一个实数![]() ,使{an}是等比数列,则有a
,使{an}是等比数列,则有a![]() =a1a3,即
=a1a3,即![]() =
=![]()
![]()
?![]()
![]()
![]() 2-4
2-4![]() +9=
+9=![]()
![]() 2-4
2-4![]()
![]() 9=0,矛盾.
9=0,矛盾.
所以{an}不是等比数列.
(2)证明 因为bn+1=(-1)n+1[an+1-3(n+1)+21]
=(-1)n+1![]()
=-![]() (-1)n·(an-3n+21)=-
(-1)n·(an-3n+21)=- ![]() bn.
bn.
又![]() ≠-18,所以b1=-(
≠-18,所以b1=-(![]() +18)≠0.
+18)≠0.
由上式知bn≠0,所以![]() =-
=-![]() (n∈N*).
(n∈N*).
故当![]() ≠-18时,数列{bn}是以-(
≠-18时,数列{bn}是以-(![]() +18)为首项,-
+18)为首项,-![]() 为公比的等比数列.
为公比的等比数列.
(3)解 当![]() ≠-18时,由(2)得:
≠-18时,由(2)得:
bn=-(![]() +18)·
+18)·![]() ,
,
于是Sn=-![]() (
(![]() +18)·
+18)·![]() .
.
当![]() =-18时,bn=0,从而Sn=0,上式成立.
=-18时,bn=0,从而Sn=0,上式成立.
要使对任意正整数n,都有Sn>12.
即-![]() (
(![]() +18 )·
+18 )·![]() >-12
>-12
?![]()
![]() <
<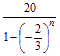 -18.
-18.
令f(n)=1-![]() ,则
,则
当n为正奇数时,1<f(n)≤![]() ;
;
当n为正偶数时,![]() ≤f(n)<1,
≤f(n)<1,
所以f(n)的最大值为f(1)= ![]() .
.
于是可得![]() <20
<20![]()
![]() -18=-6.
-18=-6.
综上所述,存在实数![]() ,使得对任意正整数n都有Sn>-12,
,使得对任意正整数n都有Sn>-12,![]() 的取值范围为(-∞,-6).
的取值范围为(-∞,-6).


科目:高中数学 来源: 题型:
| a1an+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2n |
| 3 |
| 4 |
| 9 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bn | ||
1-4
|
| 1 |
| an |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com