练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如果满足∠A=60°，BC=6，AB=k的锐角△ABC有且只有一个，那么实数k的取值范围是$（2\sqrt{3}，4\sqrt{3}）$．

    分析 依题意，可得C大于30°且小于90°，结合正弦定理解之即可．

    解答 解：由题意，30°＜C＜90°，∴$\frac{1}{2}$＜sinC＜1
    由正弦定理可得$\frac{k}{sinC}$=$\frac{6}{\frac{\sqrt{3}}{2}}$，
    ∴k=4$\sqrt{3}$sinC
    ∴k∈$（2\sqrt{3}，4\sqrt{3}）$，
    故答案为$（2\sqrt{3}，4\sqrt{3}）$．

    点评 本题考查正弦定理的运用，考查特殊角的三角函数，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．阅读程序框图，运行相应的程序，则输出s的值为（　　）
    A．0B．2C．4D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．$（a+\frac{1}{x}）{（1+x）^4}$展开式中x2的系数为0，则a=（　　）
    A．$\frac{2}{3}$B．$-\frac{2}{3}$C．$\frac{3}{2}$D．$-\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．实数m取什么值时，复数z=2m+（4-m2）i满足
    （1）z为纯虚数   
    （2）复数z对应的点位于第三象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．定义在实数集R上的奇函数f（x）满足：①f（x）在（0，+∞）内单调递增，②f（-2）=0，则不等式（x+2）f（x）＞0的解集为{x|-2＜x＜0，或 x＞2，或x＜-2 }．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在等差数列{an}中，
    （1）已知a6=10，S5=5，求S8；
    （2）已知S4=2，S9=-6，求S12；
    （3）已知a2+a4+a6=-3，a3+a5+a7=6，求S20；
    （4）已知S3=6，S6=-8，求S9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设正项等比数列{an}首项a1=2，前n项和为Sn，且满足2a3+S2=4，则满足$\frac{66}{65}$＜$\frac{{S}_{2n}}{{S}_{n}}$＜$\frac{16}{15}$的最大正整数n的值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

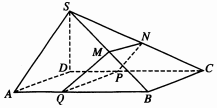    16．已知四棱锥S-ABCD的底面为平行四边形，且SD⊥平面ABCD，AB=2AD=2SD，∠DCB=60°，M，N分别为SB，SC的中点，过MN作平面MNPQ分别与线段CD，AB相交于P，Q两点（不与A，B重合）．
    （1）证明：PQ∥BC；
    （2）当平面MNPQ将四棱锥S-ABCD分成两个体积相等的多面体时，求QB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

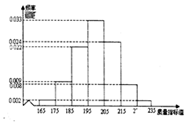    17．从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：
    （1）求这500件产品质量指标值的样本平均数$\overline x$，和样本方差s2
    （同一组数据用区间的中点值作代表）；
    （2）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N（μ，σ2），其中μ近似为样本平均数$\overline x$，近似为样本方差s2．
    ①利用该正态分布，求P（187.8＜Z＜212.2）；
    ②某用户从该企业购买了100件这种产品，记X表示100件产品中质量指标值位于区间（187.8，212.2）的产品数，利用的结果，求EX．

    查看答案和解析>>

    同步练习册答案