
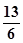 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+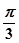 )的值.
)的值.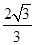 (2)
(2)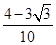
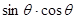 的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件:
的值,从而应用平方关系就可求得(sinθ+cosθ)2的值,再注意到θ为锐角,知sinθ+cosθ>0,开方即得所求式子的值;(2)由向量平行的坐标条件: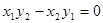 可得
可得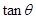 的值,法一:由
的值,法一:由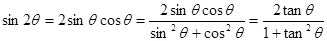 (万能公式)得到
(万能公式)得到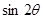 的值,同理可得
的值,同理可得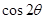 的值;再利用正弦和角公式将sin(2θ+
的值;再利用正弦和角公式将sin(2θ+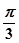 )展开即可求得其值;法二:也可由
)展开即可求得其值;法二:也可由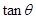 的值,应用三角函数的定义求得
的值,应用三角函数的定义求得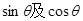 的值,进而用倍角公式可求得
的值,进而用倍角公式可求得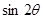 和
和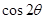 的值,下同法一.
的值,下同法一.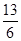 ,所以sinθcosθ=
,所以sinθcosθ=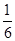 .
.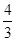 .
.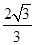 .
.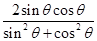 =
=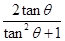 =
=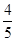 ,
,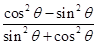 =
=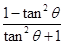 =-
=-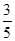 .
.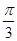 )=
)=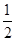 sin2θ+
sin2θ+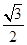 cos2θ=
cos2θ=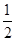 ×
×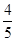 +
+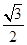 ×(-
×(-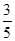 )=
)=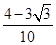 .
.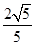 ,cosθ=
,cosθ=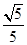 .
.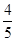 , cos2θ=cos2θ-sin2θ=-
, cos2θ=cos2θ-sin2θ=-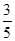 .
.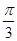 )=
)=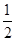 sin2θ+
sin2θ+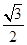 cos2θ=
cos2θ=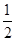 ×
×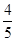 +
+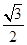 ×(-
×(-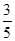 )=
)=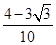 .
. 

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com