[题目]在四棱柱中. 底面.四边形是边长为的菱形. 分别是和的中点.(Ⅰ)求证: 平面,(Ⅱ)求二面角的余弦值, 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在四棱柱中，底面，四边形是边长为的菱形，分别是和的中点，

（Ⅰ）求证: 平面；

（Ⅱ）求二面角的余弦值；

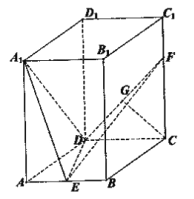
【答案】（Ⅰ）见解析（Ⅱ）

【解析】试题分析：(1)在△ADE中，利用余弦定理易得：，即又平面底面，所以平面，故，得平面；（2）以点为坐标原点，分别以所在直线为轴，建立空间直角坐标系，是平面的一个法向量，是平面的一个法向量， .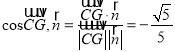

试题解析：

（Ⅰ）证明：由，结合余弦定理可得，所以

因为底面，所以平面底面

又平面底面，所以平面,

因为平面，所以 --------①

由，得

因为点是的中点，所以 --------②

由①②，得平面

（Ⅱ）由（Ⅰ）知两两垂直，以点为坐标原点，分别以所在直线为轴，建立如图所示空间直角坐标系，

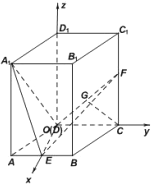
设是平面的一个法向量，则

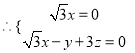,取，得,

显然，是平面的一个法向量，

由图可以看出二面角为锐角二面角，其余弦值为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= 的定义域是一切实数，则m的取值范围是（）
A.0＜m≤4
B.0≤m≤1
C.m≥4
D.0≤m≤4

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司的两个部门招聘工作人员，应聘者从 T1、T2两组试题中选择一组参加测试，成绩合格者可签约．甲、乙、丙、丁四人参加应聘考试，其中甲、乙两人选择使用试题 T1 ，且表示只要成绩合格就签约；丙、丁两人选择使用试题 T2 ，并约定：两人成绩都合格就一同签约，否则两人都不签约．已知甲、乙考试合格的概率都是，丙、丁考试合格的概率都是，且考试是否合格互不影响．
（1）求丙、丁未签约的概率；
（2）记签约人数为 X，求 X的分布列和数学期望EX．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知y=f（x）是定义在R上的奇函数，当x＞0时，f（x）=x2﹣2x．
（1）画出f（x）的简图，并求f（x）的解析式；

（2）利用图象讨论方程f（x）=k的根的情况．（只需写出结果，不要解答过程）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知圆，定点为圆上一动点，线段的垂直平分线交线段于点，设点的轨迹为曲线；

（Ⅰ）求曲线的方程；

（Ⅱ）若经过的直线交曲线于不同的两点，（点在点, 之间），且满足，求直线的方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）的定义域为D，若存在闭区间[a，b]D，使得函数f（x）满足：
①f（x）在[a，b]上是单调函数；
②f（x）在[a，b]上的值域是[2a，2b]，则称区间[a，b]是函数f（x）的“和谐区间”．
下列结论错误的是（）
A.函数f（x）=x2（x≥0）存在“和谐区间”
B.函数f（x）=2x（x∈R）存在“和谐区间”
C.函数f（x）= （x＞0）不存在“和谐区间”
D.函数f（x）=log2x（x＞0）存在“和谐区间”